\(E(X+Y)\)中\(X+Y\)到底什么意思?
我们不妨设\(X\)对应事件1,他有一个样本空间\(\Omega_{1}\),这个样本空间中的每一个事件对应一个取值
同理我们对\(Y\)也搞一个\(\Omega_{2}\)。
那么\(X+Y\)指的就是\(X\)和\(Y\)的笛卡尔积
两个集合的笛卡尔积指的是从这两个集合分别各取一个元素的所有可能的不重复的不考虑顺序的组合(注意这里不考虑顺序指的是事件顺序不考虑,比如\((e_{1},e_{2})\)和\((e_{2},e_{1})\)是同一种组合,其中\(e_{1}\)是\(X\)中的事件,\(e_{2}\)是\(Y\)的事件,但两者的映射值可能相同)
然后就可以推广到\(aX+bY\)
我们拿抛骰子举例子(就是蓝书那上面的抛两次骰子)
此时\(X\)==\(Y\)
\(X\)的样本空间为{1,2,3,4,5,6}(这里我们已经完成了映射,以映射值代替实验结果)
那么\(X+X\)==\(2X\)的样本空间就是{{1,1},{1,2},{1,3} ... {2,1},{2,2} ... {6,6}},一共三十六种
然后\(E(aX+bY)\)就是说
\(aX+bY\)这个新的事件的样本空间中的所有可能的组合,每个组合一共由\(a+b\)个映射值组成,设它们的和是sum,那么\(E(aX+bY)\)=每个组合的sum乘以这个组合的概率再将所有的组合的结果求和
这样我们只要设计出合适的映射函数就可以利用线性性来简化解题了(实际上映射函数根本不难设计)
那么对这个抛骰子的实验就可以解释了。这个实验的映射函数就是抛出了几点,对应的映射值就是几
那么正常的期望应该这么算:设某个结果为\({a,b}\),其中\(a,b\)都在1-6之间,那么\(E(2X)=\sum P({a,b})*(a+b)\)(显然任意一个\(P\)都是\(\frac{1}{36}\))
利用线性性:\(E(2X)=2E(X)\),然后就直接得出结果了
注意即使\(X\)对\(Y\)有影响也没有什么。比如抽奖,一个人先抽,后抽的人就没有办法抽到第一个人抽中的东西,但是无所谓,我们只要按照题目给的意思,把第二个人抽奖的所有可能给弄出来,然后算第一个人和第二个人抽奖的期望也可以按照线性性算的
对以上说法的严谨定义(转自这篇博客的评论)


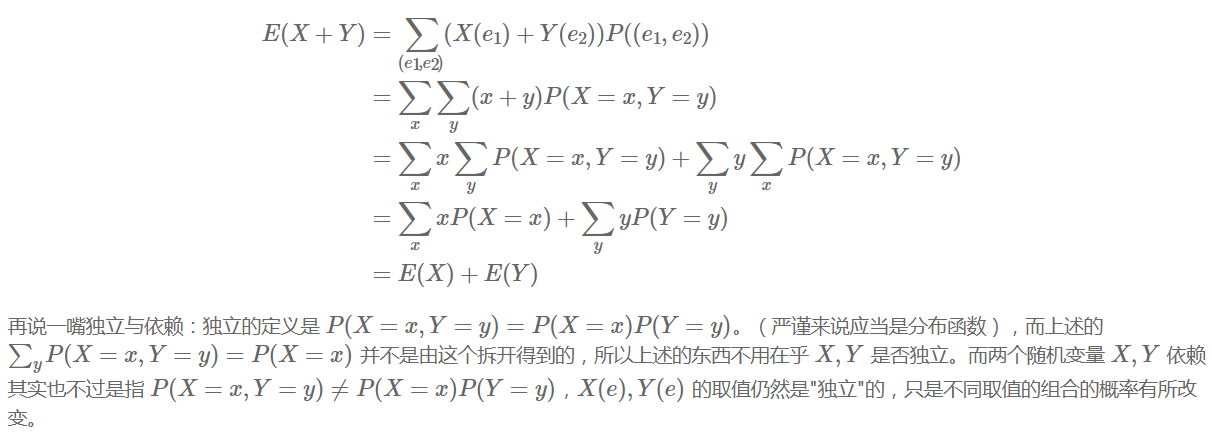
例题(见标题)
那么这一道题我们很容易想到按照题目说的从轮数去思考,设\(g[i][j]\)表示第i轮用j号牌的概率,那么\(E(X)=\sum_{i=1}^{r}\sum_{j=1}^{n}g[i][j]d[j]\)
但会发现\(g\)数组推不出来,太难推了,所以我们换一个思考对象,从牌开始思考
于是可以看这篇博客
注意所有的思考方向都要从牌那边去考虑哦
然后这篇博客考虑第二张牌那里用的是条件概率,可以理解一下