aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
每个数能取的范围是一段区间 \([l_i,r_i]\),其中 \(l_i\) 单调不增, \(r_i\) 单调不增。
画个图 (\(n=10\)):
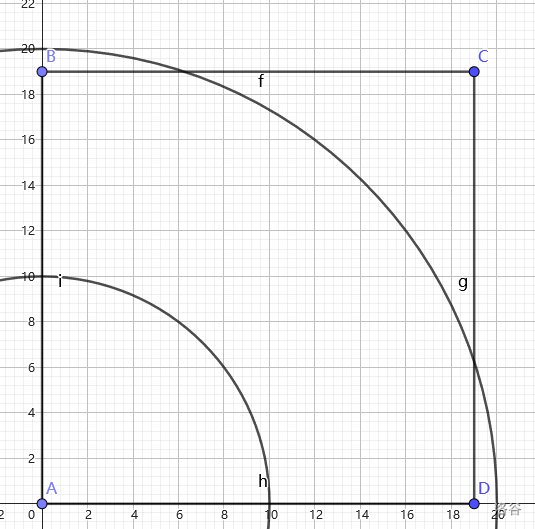
圆环和矩形的交即为合法点。
容易看出 \(l_n\) 到 \(l_{2n-1}\) 都是 0。
本质上是元素有上下界的排列计数,考虑不管下界只看上界然后容斥。
假设每个元素只有上界 \(R_i\),那么将 \(R\) 排序(记为 \(R'\)),方案数就是 \(\prod_{i=1}R'_i-i+1\)。比较好理解,每个位置能选的数的个数就是原本能选的个数减去前面已选的个数(由于有序,已选的个数就是 \(i-1\),可以发现减去的数就是排名-1)。
接下来容斥,记 \(f_i\) 为 \([0,n)\) 中恰好有 \(i\) 个的上界取 \(l_i-1\),其余上界取 \(r_i\) 的总方案数。易得 \(ans=\sum_{i=0}^n(-1)^if_i\)。
考虑求 \(f_i\)。
由于每个未知的贡献与其排名有关,不妨将序列大致排序后与过程中进行微调。
将 \([0,n)\) 部分以 \(l_i-1\) 为关键字,\([n,2n)\) 以 \(r_i\) 为关键字排序,从前往后进行 \(dp\)。设 \(dp[i][j]\) 为考虑了(排序后的)前 \(i\) 个位置,已经有 \(j\) 个 \([0,n)\) 内的位置的上界取了 \(l-1\)。
分类讨论:
- 当前点属于 \([n,2n)\):
这个点原本有 \(r_i+1\) 种选法。 \(i\) 之前所有 \([0,n)\) 中且上界取了 \(l\) 的位置都会使 \(i\) 排名 +1;还有 \(i\) 之前所有 \([n,2n)\) 的位置,由于排序,这些位置也会使 \(i\) 排名 +1。
发现第二类位置的个数(记为 \(c_1\))对于每个 \(i\) 是确定的,可以在 \(dp\) 过程中顺便记录。
于是这个位置的选法就是 \(r_i+1-j-c_1\)。
于是 \(dp[i+1][j]+=dp[i][j]\times (r_i+1-j-c_1)\)。
- 当前点属于 \([0,n)\):
又有两种情况:
上界取 \(l_i-1\):
选法是 \(l_i-j-c_1\)。原因类似上面。
于是 \(dp[i+1][j+1]+=dp[i][j]\times (l_i-j-c_1)\)。
上界取 \(r_i\):
复杂的情况。
原本有 \(r_i+1\) 种选法。
由图可得 \([n,2n)\) 所有的 \(r\) 都得排在 \(r_i\) 前面,于是排名增加 \(n\)。
最终 \([0,n)\) 内且上界取了 \(l-1\) 的所有位置都排在 \(r_i\) 前面,但是我们不知道有多少个。那么我们就设最后有 \(k\) 个,那么排名增加 \(k\)。
又由图可知,\(i\) 之前 \([0,n)\) 内且上界取了 \(r\) 的所有位置也得排在 \(r_i\) 前。与 \(c_1\) 类似,记录 \(c_2\) 为 \(i\) 之前在 \([0,n)\) 之间的个数,那么这部分排名增加 \(c_2-j\)。
于是 \(dp[i+1][j]+=dp[i][j]\times (r_i+1-n-k-c_2+j)\)。
但是由于 \(k\) 不知道,我们可以枚举 \(k\) 是多少,对每个 \(k\) 进行一次 \(dp\)。最后有 \(f_k=dp[2n][k]\)。