多面体编译技术与示例分析
多面体模型的基本概念
编译器中的多面体模型(polyhedral model)是一种高效的程序优化技术,它将复杂的循环依赖关系映射到高维几何空间,从而在编译阶段实现对计算任务的并行化和局部性优化。
通过构建和操作多面体表示能有效地调度指令和数据访问,以减少资源争用和缓存未命中德情况,从而提高程序执行的性能。
本文将介绍多面体编译技术的理论基础,并以发掘循环可并行部分为例子讲解。
将循环表示为线性不等式
首先我们来看一个常规的循环:
for (int i = 1; i < N; ++i)
for (int j = 1; j < N; ++j)
S[i][j] = ....
我们先不关注循环内执行什么语句,而是关注迭代空间 i 和 j 以及迭代限制条件:
i >= 1
i < N
j >= 1
j < N
转换为等价形式:
i >= 1
i <= N - 1
j >= 1
j <= N - 1
再统一转换为 >= 0 约束:
i - 1 >= 0
-i + N - 1 >= 0
j - 1 >= 0
-j + N - 1 >= 0
这样就将循环迭代空间表示成了一组线性不等式,然后矩阵形式表达如下:
这一组线性不等式其实就定义了二维空间上的一个矩形:

我们再来看一个例子,
for (int i = 1; i < N; ++i)
for (int j = 1; j < N; ++j)
if (i <= N - j + 1)
S[i][j] = ....
这个循环相比上面的循环就是多了一个约束条件 i <= N - j + 1 也就是 j <= -i + N + 1,也就是在上面坐标轴上再加一条线:

这样就很清楚了,这些约束的交集对应了二维空间上的一个多面体(polyhedron),同理可得如果是三层循环空间,那就是对应了三维空间上的一个多面体,每个约束条件对应一个二维平面,而在 n 维空间上就是一个超平面了。
数据依赖距离向量的定义
接着我们来介绍怎么分析循环中的数据依赖,多面体模型中的数据依赖描述了在循环结构中,不同迭代之间因数据访问而产生的依赖关系。
而对于循环嵌套内的依赖关系,可以用距离向量来描述相对执行顺序。
比如对于以下循环:
for (int i = 1; i < N; ++i)
for (int j = 1; j < N; ++j)
A[i][j] = A[i-1][j] + A[i][j-1];
在当前次 (i 和 j) 迭代中需要往 A[i][j] 中写入数据,然后需要读取 A[i-1][j] 和 A[i][j-1] 的内容也就是循环维度 i 和 j 的前一次迭代 i-1 和 j-1 需要写入的位置,所以这就引入了一个先写然后再读取的数据依赖。
然后我们定义距离向量如下,向量的值大小表示了在对应循环维度上依赖的上一次迭代的距离:
• A[i][j] -> A[i-1][j] 的距离向量为 [i - (i -1 ), j - j] = [1, 0]
• A[i][j] -> A[i][j-1] 的距离向量为 [i - i, j - (j - 1)] = [0, 1]
矩阵形式表示:
能否简单从距离向量看出循环能否并行呢?
以下讨论均假设循环都是正向且迭代步长均为1,且迭代空间为常规的整数,且不保证结论能推广。
对于该循环
for (int i = 1; i < N; ++i)
for (int j = 1; j < N; ++j)
A[i][j] = A[i-1][j] + A[i][j-1];
其距离向量为:
分析第一行可以看到i 循环维度的上,依赖了前一次迭代的计算值,所以可以知道在 i 循环上无法并行。
而分析第二行依赖,j 循环维度也依赖了前一次迭代的计算值,所以可以知道在 j 循环上也无法并行。
又比如对于循环
for (int i = 1; i < N; ++i)
for (int j = 1; j < N; ++j)
A[i][j] = 0;
其距离向量为 [0]。
循环维度 i 和 j 对于前面的循环没有任何依赖,所以能将两个循环合并为一个然后并行运行。
又比如对于循环
for (int i = 1; i < N; ++i)
for (int j = 1; j < N; ++j)
A[i][j] = A[i][j-1];
其距离向量为 [0, 1]。循环维度 i 无依赖可以在该维度上并行,但是在 j 维度上有依赖无法并行。
又比如对于循环
for (int i = 1; i < N; ++i)
for (int j = 1; j < N; ++j)
A[i][j] = A[i-1][j] + A[i-1][j-1];
其距离向量为:
两个依赖的循环维度 i 都是大于0,所以在 i 维度无法循环,但是在 j 维度却可以并行。所以只要第一列都大于0,则不用分析第二维了,第二维是一定可以并行的。
有些循环的距离向量没法直接看出来,比如经典的矩阵乘法:
for (int i = 0; i < N; ++i)
for (int j = 0; j < N; ++j)
for (int k = 0; k < N; ++j)
C[i][j] = C[i][j] + A[i][k] * B[k][j];
这里在循环维度 k 上有个隐式的依赖,当前迭代(i', j', k') 的 C[i'][j'] 计算依赖于上一次迭代 (i', j', k'-1) 计算得到的 C[i'][j'],所以距离向量为 [0, 0, k-(k'-1)=1],所以在k 维度上无法并行。
对循环做变换
多面体模型中对循环优化是通过对循环迭代空间做仿射变换实现的,下面我们介绍三种简单的变换,交换和倾斜。
以二层循环为例:
for (int i = 1; i <= 2; ++i)
for (int j = 1; j <= 3; ++j)
S[i][j] = ...
对应的每一次迭代的执行顺序如下图,图中的圆型就对应每一次的迭代,序号就是原始执行顺序:

假设变换后的循环维度分别是 i' 和 j'。
循环交换
对应的变换矩阵如下:
变换过程如下:
对应的循环就变为:
for (int j = 1; j <= 3; ++j)
for (int i = 1; i <= 2; ++i)
S[i][j] = ...
对应的迭代执行顺序如下:
图中圆型的序号为变换前的原始执行顺序。
第一个执行的坐标是 (i'=1, j'=1),对应原始坐标是 (i=1, j=1),对应圆型 1。
第二个执行的坐标是 (i'=1, j'=2),对应原始坐标是 (i=2, j=1),对应圆型 4。
第三个执行的坐标是 (i'=2, j'=1),对应原始坐标是 (i=1, j=2),对应圆型 2。
其他以此类推
循环反转
对应的变换矩阵如下,假设就对循环 i 做反转:
对应的变换矩阵如下,假设就对循环 i 做反转:
变换过程如下:
对应的循环就变为:
for (int i = -1; i >= -2; --i)
for (int j = 1; j <= 3; ++j)
S[i+3][j] = ...
对应的迭代执行顺序如下:

图中圆型的序号为变换前的原始执行顺序。
第1个迭代 (i'=-1, j'=1) 对应原始坐标 (i=2, j=1) ,对应原始循环的圆型 4 。
第4个迭代 (i'=-2, j'=1) 对应原始坐标 (i=1, j=1) ,对应原始循环圆型 1 。
循环倾斜
对应的变换矩阵如下:
变换过程如下:
对应的循环就变为:
for (int d = 2; d <= 5; ++d)
for (int j = max(1, d - 2); j <= min(3, d - 1); ++j)
int i = d - j;
S[i][j] = ...
对应的迭代执行顺序如下:


图中圆型的序号为变换前的原始执行顺序。
第1个迭代 (d=2, j=1) 对应原始坐标 (i=1, j=1) ,对应原始循环的圆型 1 。
第2个迭代 (d=3, j=1) 对应原始坐标 (i=2, j=1) ,对应原始循环圆型 4 。
第3个迭代 (d=3, j=2) 对应原始坐标 (i=1, j=2) ,对应原始循环圆型 2 。
第4个迭代 (d=4, j=2) 对应原始坐标 (i=2, j=2) ,对应原始循环圆型 5 。
第5个迭代 (d=4, j=3) 对应原始坐标 (i=1, j=3) ,对应原始循环圆型 3 。
第6个迭代 (d=5, j=3) 对应原始坐标 (i=2, j=3) ,对应原始循环圆型 6 。
如何将串行执行的循环转换为可并行执行
以下面的循环为例:
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
A[i][j] = A[i-1][j] + A[i][j-1];
}
}
分析上其数据依赖分析可得其距离向量:
可知该循环在 i 和 j 维度上都无法并行执行。
接下来尝试对循环空间 i 和 j 做仿射变换,我们采用倾斜变换,其实这个是很经典的一个并行方法了,称之为对角线变换。
具体到多面体编译技术的代码的实现,是怎么自动找到这个变换的过程我还没完全弄懂,所以假设我们现在知道了是直接应用倾斜变换:
代码变为:
for (int d = 2; d <= 2 * N; ++d) {
for (int j = max(1, d - N); j <= min(N, d - 1); ++j) {
int i = d - j;
A[i][j] = A[i-1][j] + A[i][j-1];
}
}
接着分析数据依赖矩阵,这时候 A[i][j]= A[d-j][j] 的计算都只依赖于循环 d 前一次迭代的计算而循环 j 维度上没有数据依赖,所以依赖矩阵为:
从依赖矩阵可知,变换后的循环可以在 j 循环维度上做循环。
上面的文字解释可能有些抽象我们画图来辅助解释,假设循环上界 N=5,则原始的循环迭代空间如下图所示:

黑色实线箭头表示每个计算 A[i][j] 的计算顺序。
数据依赖关系如下:

红色箭头表示数据依赖。
则经过倾斜变换后的循环迭代空间如下:
for (int d = 2; d <= 2 * 5; ++d) {
for (int j = max(1, d - 5); j <= min(5, d - 1); ++j) {
int i = d - j;
A[i][j] = A[i-1][j] + A[i][j-1];
}
}
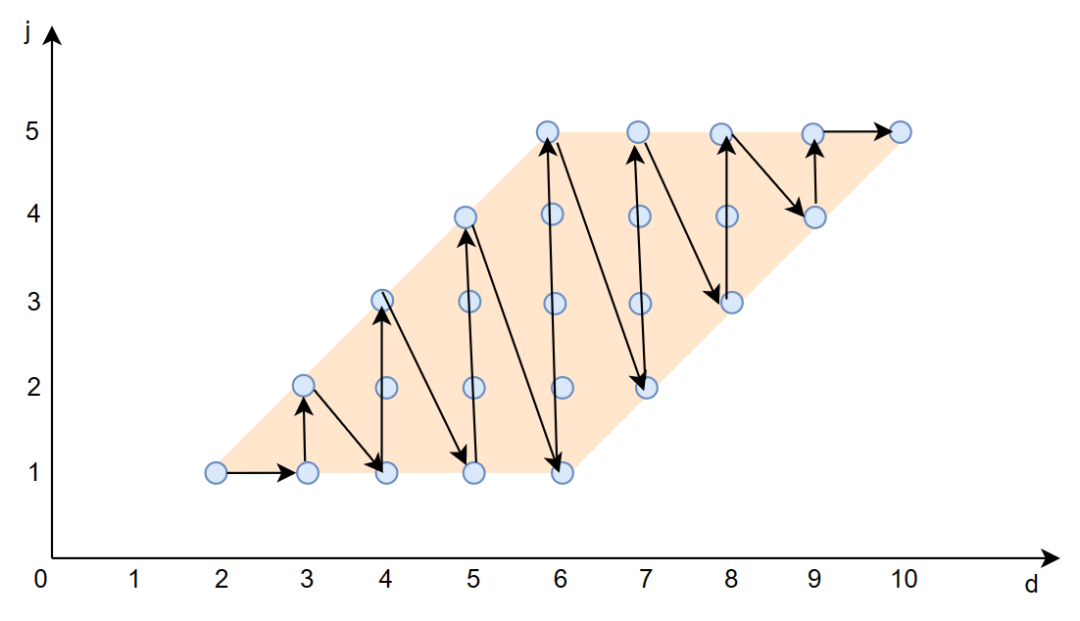
其实就是对应于原始空间上,按照对角线的顺序去遍历。
数据依赖如下:

从数据依赖上看,可以看到变换后在 j 维度上没有数据依赖所以可以并行执行。
最后在 j 维度上加上 omp 并行:
for (int d = 2; d <= 2 * 5; ++d) {
#pragma omp for
for (int j = max(1, d - 5); j <= min(5, d - 1); ++j) {
int i = d - j;
A[i][j] = A[i-1][j] + A[i][j-1];
}
}
这篇文章中对于多面体模型有并不少是个人理解,不一定准确。多面体编译技术个人感觉很复杂,在阅读相关文献和书籍的时候,还需要去搜过相关前置知识才能看懂大概。
而这篇学习笔记也仅仅是介绍了一些基本的入门概念,多面体编译技术能做的事情并不仅仅局限于本文所介绍的循环变换发掘可并行部分,感兴趣的读者可以阅读参考资料。
MLIR编译器的多面体优化
摘要
多面体编译是一项成熟的编译优化技术,演进了几十年,在传统的编译器中常作为一种优化工具使用,比如LLVM中使用的Polly,在GCC中使用的GRAPHITE。近些年来,多面体技术也引入到AI编译器中,进行循环优化及算子融合优化等。将关注在MLIR中以类插件的形式引入多面体优化技术,补充其多面体优化能力。
多面体模型的介绍
多面体模型(Polyhedral)主要关注的是程序设计中的循环优化问题,两层循环的循环变量的取值范围可以构成一个平面,三层循环的循环变量可以组成一个长方体,如图1所示,因此得名多面体模型。

图1 不同循环层次的多面体表示[1]
多面体编译优化关注的是在确保程序执行正确的前提下重组多重循环的结构,实现性能的最优化。比如图2的循环中,左图表示的原始的二维迭代空间,蓝色箭头表示数据(黑点)之间存在依赖关系,对角线的绿色表示数据没有依赖关系,经过变基操作之后变为右图的表达式及迭代空间,从形状看像是把多面体进行了变形,形象地体现出多面体优化的过程。当然,变形的目的是为了实现并行计算,达到更好的性能,具体分析可以参考[1][2]。

图2 多面体的变基转换及Affine_map表示[2]
MLIR中的多面体表示
MLIR关于多面体的设计重表达轻优化,也就是说MLIR充分利用其IR的特性定义了表示多面体的方言Affine[3],而没有进行多面体的优化实现。这样做的目的符合MLIR重在编译器基础设施搭建的特性,而具体的实现可以自行定义,好比MLIR向用户交付了布局合理的毛坯房,内部装修各取所好。另外,关于多面体优化的工具也很成熟,各种开源工具齐全,比如isl[4],Polly[5],Pluto[6],以及CLooG[7],也为将编译优化工具引入到MLIR提供了便利。MLIR中Affine方言的定义使用具有多面体特征的循环和条件判断来表示,显示地表示静态控制部分(SCoP:Static Control Part),比如affine.for, affine.if, affine.parallel等,具体可以参见官方文档[3]。在Affine的表达中,使用Dimension和Symbol两类标识符,二者在MLIR语法中均为index类型,同时MLIR也对这两类表示进行约束有助于提升分析和转换能力。从表示形式上看,Dimension以圆括号来声明,Symbol用方括号声明,Dimension即字面意思表示仿射对象的维度信息,比如映射,集合或者具体的loop循环以及一个tensor,Symbol表示的是多面体中的参数,在编译阶段是未知的。在准线性的分析表达上,Symbol当作常量对待,因此Symbol和Dimension之间可以进行乘加等线性操作,但Dimension之间的操作是非法的。另外,Dimension和symbol都遵从SSA赋值。MLIR的Affine重表达体现在通过具体的映射可以表示出多面体的变换,比如图1中的变基操作,通过affine_map语句就能够体现出来。矩阵计算中常用的关于内存的tiling操作,也可以通过affine_map表示。通过#tiled_2d_128x256 = affine_map<(d0, d1) -> (d0 div 128, d1 div 256, d0 mod 128, d1 mod 256)>可以表示如下图所示的tiling切分。X维度按照128个元素,Y维度按照256维度进行tiling切分,形成了x.outer和y.outer,内部的取模运算计算在单个tiling内部的偏移量,形成x.inner和y.inner。图4中表示采用Affine方言表示多项式乘法C[i+j] += A[i] * B[j],从中可以明确看到和多面体相关的操作表达。

图3 tiling的操作

图4 多项式乘法的Affine方言表示
MLIR中引入多面体优化
Polygeist[9]文章沿用LLVM引入Polly,GCC引入GRAPHITE的思路,将开源的Pluto引入到MLIR中实现多面体优化。整体的编译采用LLVM的编译流程,前端Clang分析输入的C语言代码,转换到MLIR中的Affine方言,然后从Affine转换到Pluto,二者之间的交互采用多面体技术中常用的数据格式OpenScop[8],优化后的代码再次转换到MLIR,然后走LLVM的编译流程。在整体的转换中,使用的方法就是遍历语法树(AST)。Clang前端遍历Clang的AST语法树,将node映射到MLIR的操作中;从Pluto到MLIR的转换过程中使用CLooG生成初始循环的AST,然后遍历AST中的node,创建与循环和条件判断相对应的MLIR的操作。这种做法可以产生和现有编译器的应用程序二进制接口(Application Binary Interface)兼容的代码,免去重新构建基础设施。Polygeist出彩的地方的是将C/C++引入到了MLIR,实现了clang前端对MLIR的对接,利用MLIR的IR变换能力对接到开源的Pluto工具进行多面体的优化。从整体的测试效果看,优化的性能没有得到特别显著的提升,原因在于针对benchmark中的实例,现有的编译工具已经优化的很好,比如LLVM对于Clang前端的IR能够减少特定的load操作,而LLVM对MLIR的IR还不支持此优化功能,MLIR还是相对比较新鲜的事物。正如文中所言,使用MLIR生成比多面体工具更加优化的代码不是该工作的兴趣点,而是证实在MLIR中引入多面体优化工具的灵活性。当然,整体的转换工作不是一蹴而就的,需要涉及到C语言和MLIR之间类型的转换,目前支持的数据类型如图5所示,不支持struct的数据类型,同时也不支持C语言中的break操作。在MLIR中没有指针的概念,关于内存的表示只有memref,MLIR本身也不支持在memref中嵌套memref,为了对接C语言中的指针的指针,文章增加对memref的嵌套使用,也就是修改了原有MLIR的特性。

图5 C语言,LLVM IR和MLIR数据类型的对应关系
整体实现的流程如图6所示,前端搭建了C代码到MLIR的连接,通过遍历Clang的AST语法树,将每个访问的节点映射到MLIR中的SCF或者standard方言中的操作。MLIR起到表达控制流的作用,在方言的表达中直接查找到循环,减少在Pluto的CFG (Control Flow Graph) 中查找loops循环的必要。但是实际上,Pluto还是参与了C/C++中非线性for循环的查找。AST中C语言的数据类型先是转换到LLVM的数据类型,然后转换到MLIR中Standard方言中的数据类型。
多面体相关的Affine code转换通过识别标识符将#pragma scop和#pragma endscop表示的code直接转化为affine.for 循环。循环约束以affine_map的形式表示,比如(affine_map<()[s0]->(s0)>[%bound]),()中表示的是表示Dimension,[ ]表示的是Symbol,如前文所言。
前端输入的C语言经过转换到MLIR-SCF方言层级,通过raise-affine的PASS转换为Affine方言,具体实现的功能是将standard 方言中的load, store,SCF方言中的for和if转换到affine方言中对应的操作。利用Pluto的能力进行优化处理,然后再通过low-affine PASS转回到MLIR-SCF,此处借助CLooG进行语法树分析,然后走MLIR的LLVM编译流程。

图6 Polygeist的编译流程
结论与思考
现有的多面体优化的库,比如isl,Polly,主要用于C语言的source-source转换,聚焦于底层级的优化,无法直接用在MLIR的设计中,因为底层级的表示无法还原完整的高层级的表达。Polygeist的工作将MLIR的多面体表示和现有的高层级的优化工具结合起来,采用MLIR Affine方言和OpenScop数据格式的双向转换方便开发者搭建基于MLIR的编译流程,然后使用现有的多面体优化工具优化,最后返回到MLIR进行进一步的转换并最终生成代码。对于我们的启发在于可以在MLIR中引入其他优化工具助力编译优化,根据需求补足MLIR中缺失的能力。
多面体优化是一项成熟的技术,但也受限于对仿射变换的依赖,对无法进行仿射的循环的优化能力较弱,存在一定的局限性,因此无法在工业界得到广泛应用。同时,多面体优化技术理论相对复杂难懂,从事相关研究的人员较少,难以进行落地。尽管如此,多面体技术在解决特定的问题方面尤其独特的作用,比如在深度学习领域,对多算子融合和多层循环优化方面有着极大的帮助,可以将现有的多面体技术引入到AI编译器中,进行特定功能的优化。
参考文献链接https://mp.weixin.qq.com/s/6y7AfPcpIT_XB2f9MPicNA
https://mp.weixin.qq.com/s/n33DyOeTjA93HavZBZb94g
[1] Uday Bondhugula, Polyhedral Compilation Opportunities in MLIR http://impact.gforge.inria.fr/impact2020/slides/IMPACT_2020_keynote.pdf
[2] 要术甲杰, Polyhedral Model—AI芯片软硬件优化利器https://mp.weixin.qq.com/s?__biz=MzI3MDQ2MjA3OA==&mid=2247485130&idx=1&sn=a5773bf17e6854d1238b035366641bcc&chksm=ead1fbdbdda672cdf9b2480a431cef85e4d377d07f8c586a932adabd50656cbdcd7d891156bf&mpshare=1&scene=1&srcid=&sharer_sharetime=1569677798809&sharer_shareid=b33ef36fa0caf5cb82e76916516aa7df#rd
[3] https://mlir.llvm.org/docs/Dialects/Affine/#affine-maps
[4] Sven Verdoolaege. 2010. isl: An integer set library for the polyhedral model. In International Congress on Mathematical Software. Springer, 299–302
[5] Tobias Grosser, Armin Groesslinger, and Christian Lengauer. 2012. Polly—performing polyhedral optimizations on a low-level intermediate representation. Parallel Processing Letters 22, 04 (2012), 1250010.
[6] Uday Bondhugula, Albert Hartono, Jagannathan Ramanujam, and Ponnuswamy Sadayappan. 2008. A Practical Automatic Polyhedral Parallelizer and Locality Optimizer. ACM SIGPLAN Notices 43, 6 (2008), 101–113.
[7] Uday Bondhugula, Albert Hartono, Jagannathan Ramanujam, and Ponnuswamy Sadayappan. 2008. A Practical Automatic Polyhedral Parallelizer and Locality Optimizer. ACM SIGPLAN Notices 43, 6 (2008),
101–113.
[8] Cédric Bastoul. 2011. Openscop: A specification and a library for data exchange in polyhedral compilation tools. Technical Report. Paris-Sud University.
• [1] 《多面体编译理论与深度学习实践》
• [2] http://web.cs.ucla.edu/~pouchet/index.html#lectures
• [3] https://web.cs.ucla.edu/~pouchet/software/pocc/