题目大意

给定一个带权无向图与距离 \(t\)，问有多少条从 \(1\) 到 \(n\) 路径长度为 \(T\)。

思路

从特殊情况出发

先考虑权值只有 \(0,1\) 的情况，我们设 \(f_t[i][j]=k\) 代表从 \(i\) 到 \(j\) 经过的路径权值综合为 \(t\) 的方案数共 \(k\) 种。

那么我们可以在 \(1\cdots n\) 中任选一点作为中转站，推出转移式 \(f_t[i][j]=\displaystyle\sum_{k=1}^{n} f_{t-1}[i][k]+f_1[k][j]\)，即 \(f_t=f_{t-1}\times f_1\)。

显然，我们想到了矩阵乘法快速幂，这样就可以快速地求方案数了。

将普通情况转化为特殊情况

但是，题目中的权值范围不仅仅是 \(0,1\) 还包括了 \([0,9]\in \mathbb{Z}\)。

因为权值范围较小，所以考虑把点拆开，强行转化为边权只有 \(0,1\) 的情况。

如图，我们把点拆为 \(9\) 个点，其中只有编号 \(0\) 的点代表了原来的点，其余点均向编号小一的点连一条权值为 \(1\) 的边。

连边我们就可以用如下图的方式连边。

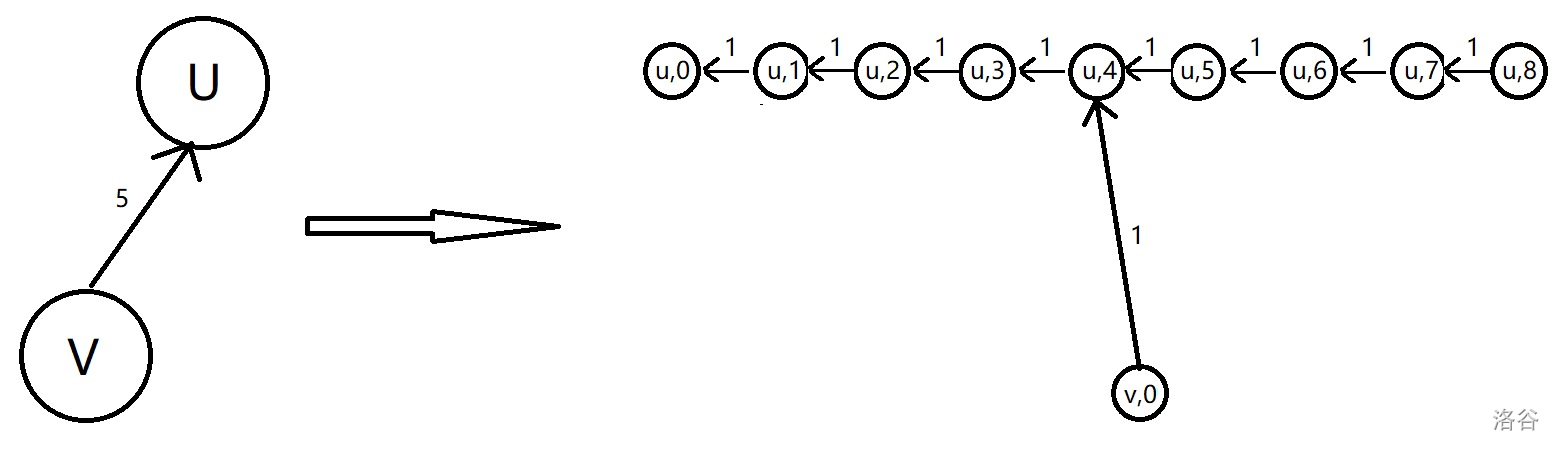
我们可以发现，代表 \(v\) 的真正点与代表 \(u\) 的真正点距离与原来一样，而边权就被强制转化为 \(1\) 了。

至此，问题就被分为了两个部分，其一，拆点建图；其二，矩阵乘法快速幂。

AC 代码

#include<bits/stdc++.h>
using namespace std;
const int mod=2009;
int n,N,t;
char c[15];
struct node{int a[150][150];}a;
node operator *(node a,node b)//矩阵乘法
{
	node ans;
	memset(ans.a,0,sizeof(ans,a));
	for(int i=1;i<=n;++i) for(int j=1;j<=n;++j) for(int k=1;k<=n;++k) ans.a[i][j]=(ans.a[i][j]+a.a[i][k]*b.a[k][j])%mod;
	return ans;
}
node operator ^(node a,int b)//矩阵乘法快速幂
{
	node ans;
	memset(ans.a,0,sizeof(ans.a));
	for(int i=1;i<=n;++i) ans.a[i][i]=1;
	while(b)
	{
		if(b&1) ans=ans*a;
		a=a*a;b>>=1;
	}
	return ans;
}
int main()
{
	scanf("%d%d",&n,&t);
	N=n,n*=9;
	for(int i=1;i<=N;++i) for(int j=1;j<=8;j++) a.a[9*(i-1)+j][9*(i-1)+j+1]=1;//拆点
	for(int i=1;i<=N;++i)
	{
		scanf("%s",c+1);
		for(int j=1;j<=N;++j) if(c[j]>'0') a.a[9*(i-1)+c[j]-'0'][9*(j-1)+1]=1;//强制转化边
	}
	a=a^t;//快速幂
	printf("%d",a.a[1][N*9-8]);//得出结果
	return 0;
}