526互联

AcWing算法基础课 数学知识（二）

发布时间 2023-03-28 22:36:07作者: Pan_ma_ru

一、欧拉函数

公式及其简单的证明

image

欧拉定理

若\(a\)与\(n\)互质，则有\(a^{\phi(n)} \equiv 1 (mod \quad n)\)

简单证明

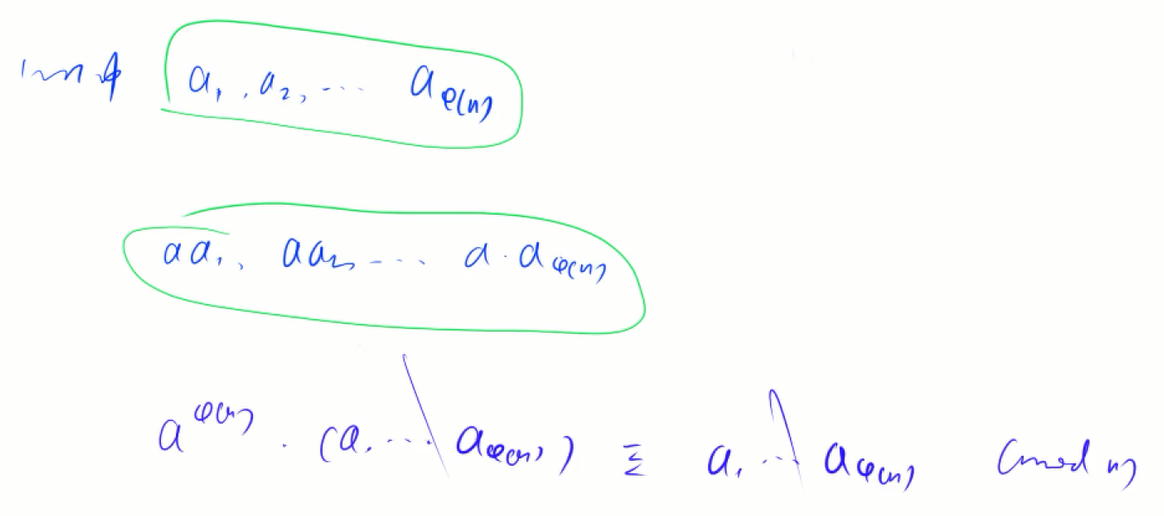
image

定义求欧拉函数

时间复杂度\(O(\sqrt{n})\)

int phi(int n)
{
    int res = n;
    for (int i = 2; i <= n / i; ++ i)
    {
        if (n % i == 0)
        {
            res = res / i * (i - 1);
            while (n % i == 0) n /= i;
        }
    }
    if (n > 1) res = res / n * (n - 1);
    return res;
}

筛法求欧拉函数

若\(i\)为质数，则\(\phi(i) = i - 1\);

若\(i\)不为质数，且\(prime[j]\)为\(i\)的约数，则\(\phi(i) = primes[j] * \phi(i)\);

若\(i\)不为质数，且\(primes[j]\)不为\(i\)的约数，则\(\phi(i) = (primes[j] - 1) * \phi(i)\);

特别情况下，当\(i\)为1时，\(\phi = 1\)

时间复杂度\(O(n)\)

void euler(int n)
{
    phi[1] = 1;
    for (int i = 2; i <= n; ++ i)
    {
        if (!st[i]) primes[cnt ++ ] = i, phi[i] = i - 1;
        for (int j = 0; primes[j] <= n / i; ++ j)
        {
            st[primes[j] * i] = 1;
            if (i % primes[j] == 0)
            {
                phi[i * primes[j]] = phi[i] * (primes[j]);
                break;
            }
            phi[i * primes[j]] = phi[i] * (primes[j] - 1);
        }
    }
}

二、快速幂

时间复杂度\(O(logn)\)

int qpow(int a, int k, int mod)
{
    int res = 1;
    a %= mod;
    while (k)
    {
        if (k & 1) res = res * a % mod;
        k >>= 1;
        a = a * a % mod;
    }
    return res;
}

三、求逆元

\(a\)、\(p\)互质，\(a \cdot a^{-1} \equiv 1 (mod \quad p)\)，在取余意义下，除以一个数等价于乘以这个数的逆元

若\(p\)为质数，\(a^{-1} = a^{p - 2}\)；

若\(p\)不为质数，利用扩展欧几里得算法求\(a^{-1}\)

例题：AcWing 快速幂求逆元

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

ll gcd(ll a, ll b, ll mod)
{
    ll ans = 1;
    a %= mod;
    while (b)
    {
        if (b & 1) ans = ans * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return ans;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    
    int n;
    cin >> n;
    while (n -- )
    {
        ll a, p;
        cin >> a >> p;
        if (a % p) cout << gcd(a, p - 2, p) << '\n';
        else cout << "impossible\n";
    }
    
    return 0;
}

四、裴蜀定理

对于任意正整数\(a\)、\(b\)，一定存在非零整数\(x\)、\(y\)，使得\(ax + by = gcd(a, b)\)，所有\(a\)和\(b\)所能凑出来的数一定很为\(gcd(a, b)\)的倍数

五、扩展欧几里得算法

给定正整数\(a\)、\(b\)，求一组\(x\)、\(y\)使得\(ax + by = gcd(a, b)\)

时间复杂度\(O(logn)\)

int exgcd(int a, int b, int &x, int &y)
{
    if (!b)
    {
        x = 1, y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}

六、线性同余方程

给定\(a\)、\(b\)、\(m\)，求出一个 \(x\)，使其满足 \(ax \equiv b (mod \quad m)\)

时间复杂度\(O(logn)\)

例题：AcWing 线性同余方程

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

ll exgcd(ll a, ll b, ll &x, ll &y)
{
    if (!b)
    {
        x = 1, y = 0;
        return a;
    }
    ll d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    
    int n;
    cin >> n;
    while (n -- )
    {
        ll a, b, m, x, y;
        cin >> a >> b >> m;
        ll d = exgcd(a, m, x, y);
        if (b % d) cout << "impossible\n";
        else cout << x * b / d % m << '\n';
    }
    
    return 0;
}

七、中国剩余定理

image