膜拜 hhj 大佬。
分块
对于分块的数据结构,往往是用来解决其它线性数据结构以及树形数据结构难以解决的问题,由此,分块也被冠以“终极数据结构”的称号。
1.块状数组
块状数组,即把一个数组分为几个块,块内信息整体保存,若查询时遇到两边不完整的块直接暴力查询,块的大小通常为 \(O(\sqrt{n})\)。
分块的难点因题而异,重要的是抓住分块对时间复杂度的宽容性。
例如,修改整个块的复杂度需要为 \(O(1)\),而修改不完整块的复杂度一般是暴力修改 \(O(\sqrt{n})\),然而暴力重构整个块的复杂度也是 \(O(\sqrt{n})\),这启示我们在单点暴力修改也相当困难时可以直接重构整个块。
例题就直接用 \(小 ω 的树\) 吧,Kruskal重构树上维护分块,块内维护斜率优化的单调栈,不完整块直接重构,遍历所有块查询。
2.块状链表
平衡树太难调了,什么人会在考场上调平衡树啊。
对于插入的操作,分块也可以解决部分。与块状数组类似,块状链表将原数组按照 \(\sqrt{n}\) 个一组分为 \(\sqrt{n}\) 组,每组组内维护一个数组。
块状链表在插入时可以 \(O(\sqrt{n})\) 地寻找要插入的块, \(O(\sqrt{n})\) 地插入。注意到在同一块内插入次数过多时,可能导致块的大小超标,从而导致超时,下面给出 \(3\) 种解决方案。
- 定期重构。可以在每进行 \(\sqrt{n}\) 次插入操作后重构整个数组,时间复杂度在均摊意义下是不变的。
- 超限重构。在某个块大小超过 \(2\sqrt{n}\) 后重构整个数组,复杂度与上一种相同,常数更优。
- 超限分裂。在某个块大小超过 \(2\sqrt{n}\) 后分裂这个块,若使用链表维护每个大块之间关系,重构常数可以更小。
但是 \(NOIP\) 的题目并不卡常,所以在代码难度的角度看,超限分裂的方法并不很常用。
当然如果正解并不是分块,想拿到高分就要好好考虑考虑代码的常数大小了。
例题 \(POJ2887\) ,单点插入单点查询,相当板子了。平衡树当然能做,但是你真的不试试分块的暴力美学吗。
树状数组
恕我直言,树状数组能做的线段树全都能做。
所以树状数组相较于线段树而言,更优的就只有它优秀的时间复杂度了。树状数组的查询复杂度本质上是 \(O(popcnt(x))\) 的,而修改则是 \(x\) 在 \(n\) 范围内的补集的 \(popcnt\) ……总而言之,树状数组的时间复杂度中,\(\log{n}\)只是它的上界。
树状数组的修改和查询有两种理解方式,一种是后缀修改+单点查询,一种是单点修改+前缀查询。两种理解方式的不同可能会导致运用思维的不同,甚至关系到能否解出题目。
例题 \(P1168\) ,求前奇数个的中位数,离散化然后树状数组上二分即可。平衡树和权值线段树也可做,但是这是黄题。这题做法相当多,很多数据结构都支持。
线段树
线段树在数据结构题中出现频率还是相当高的。毕竟平衡树太长,树状数组我们有时候又不当做数据结构题。
普通的线段树,单点修改区间修改,单点查询区间查询,支持的很多,主要难度还是体现在 \(pushdown\) 的标记下传和 \(pushup\) 的区间合并上——总而言之,就是维护的数据的设计。这些还是比较吃思维,想到了就是想到了,想不到也没办法,种类太多了。
所以这里还是讲其它的线段树的方法。
1.线段树合并
从根到叶,把同时存在的点合并,非同时存在时直接把这颗子树取走。
看到 “存在的点” 就知道线段树合并一般是在动态开点的权值线段树上打的。
例题 \(P4556\) ,路径带种类加,求每点最多的种类,树上查分,对每点建一颗动态开点线段树最大值及其编号,上传时合并即可。
2.可持久化线段树
每次进行修改时维护新树的节点,将需要修改的点新建,并将原来的子树连上,就可以在不改动原树的情况下新维护一颗树。注意若是区间修改,不能直接 \(pushdown\) 而应该标记永久化,否则可能造成新点下传影响旧点的情况。
可持久化线段树的亮点除了可以查询历史版本以外,还在于部分在区间上和树上的性质。例如可以以数组下标为时间,用作差的方式维护区间信息,或者在树上维护路径信息。
例题 \(HDU 2665\) ,求区间第 \(k\) 大,如上述维护权值线段树,查询时作差即可。
3.线段树套线段树
用线段树去维护树上信息是相当经典的线段树用法。维护的信息不太难时,可以直接树剖然后用普通的线段树;维护的信息较难但是可以离线查询时,可以尝试线段树合并或者可持久化线段树来维护子树信息或者路径信息。但是如果维护的信息较难而且需要在线时,或许可以试试看树套树。为什么不试试终极数据结构呢。
具体来说就是在每个线段树节点上开一颗线段树。当然,两颗线段树中往往至少有一颗是动态开点的权值线段树。这里有个小盲区,可能认为外层的线段树一定是是在序列上二分的,实际上外层使用值域上二分的权值线段树或许能够维护更多信息。你问我这和上面说的树上问题有什么关系?树上问题在树剖之后不久转成序列上问题了嘛。
注意线段树套线段树时一般不会有 \(pushup\) 操作,因为在每个节点上的线段树上直接修改几乎总是比从儿子合并上来更快。
例题 \(P3380\) ,区间查询排名,第 \(k\) 大,前驱后继,单点修改。权值线段树套线段树,直接解决。
单调队列
单调队列维护队列性质的同时维护单调性。做法很简单,来看题目。
例题 \(P1440\) ,维护某数前 \(m\) 个数中的最小值。单调队列里面放下标,每次插入值前把队尾大于该值的点删除,删除队首已经过时的点,就能保证每次队首值就是区间最小值。可以用 \(deque\) 维护单调栈,也可以使用数组模拟,需要插入多少点就开多大的数组。
例题 \(OJ2084\) ,暴力可以用单调队列打,由于花费小的地牢总比前面的花费大的地牢更好,但是在买能量的时候会有一个阈值,所以维护一个单调队列,队内花费单调递增。具体可以看\(我的暴力\) 。
单调栈
几乎同上,不过维护的变成队列性质了。
和队列不同,单调栈是先进后出的,所以对于每一个塞进栈里的点,都应该在删除时或者仍旧存在于栈里的时候可以做出贡献,否则直接用单个变量维护最值即可。
例题 \(P2866\) ,问每个点右侧第一个权值大于当前点的点与当前点的距离-1之和,模拟一个从栈底到栈顶单调递减的单调栈,将当前点弹出的点即第一个大于当前点的点。
斜率优化
斜率优化可以优化 \(dp\) ,但本质上实际是维护一个下凸包,所以讲一下。
把 \(dp\) 式子写成数个一元函数的最小值,维护单调栈时需要按照斜率升序排序,查询时二分最小值。注意单调栈的弹出条件并非在某个特定的点上某条线大于另一条,而是要时刻维护栈内的二分性质,忘记这个很容易导致算法假掉。
并查集
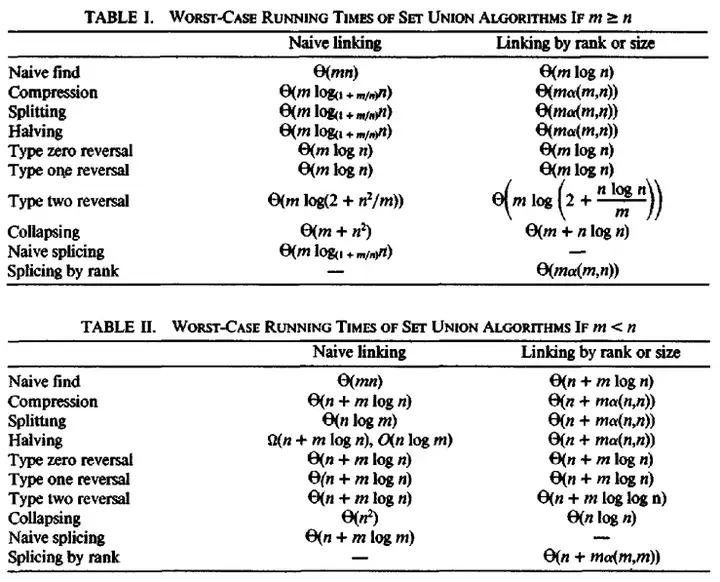
没有路径压缩和启发式合并的并查集操作是 \(O(nm)\) 的,只没有启发式合并的并查集操作是 \(O(m\log {n})\) 的,只没有路径压缩的并查集操作是 \(\Omega(m\log_{1+\frac{m}{n}}{n})\) 的,但在平均情况下与两者兼有时相同,而两者兼有的并查集操作是 \(\Theta(m\alpha(n))\) 的。具体证明详见 \(OI Wiki\) ,但是最好别看,是势能分析。
普通的并查集若要支持单个元素的删除或移动操作,需要预先给每个节点制作副本,并将副本作为父亲,以保证自身永远是叶子。可以用动态开点线段树实现可持久化并查集。并查集不支持较低复杂度的集合分离。
并查集可以拿来跑最小生成树,没什么好讲的就不讲了。
扩展域并查集
扩展域并查集,实际上就是给并查集的点开多倍的技巧。使用时将 \(i\) ,\(i+n\) ……作为一个整体,按照题意维护点之间的关系,并保证同一个整体内的点总是不在一个并查集中。
可以拿来跑二分图的判断,但是我们还可以做这题:
例题 \(P2024\) ,开 \(3\) 倍的并查集,维护吃与被吃的关系,判断假话。
权值并查集
在对并查集进行路径压缩和合并操作时,这些权值具有一定属性,即可将他们与父节点的关系,变化为与所在树的根结点关系。
权值并查集是每个点带权的并查集,这个权值可以是所有儿子的元素和,也可以是该点与父亲的关系,或者是其他的什么。根据权值种类的不同,一个点的权值在合并,删除,移动甚至是路径压缩的时候改动。
例题 \(UVA11987\) ,需要支持合并,单点移动,查询集合大小以及元素和。每个点开副本,令父亲为副本,在根节点位置记元素和。
例题 \(P2024\) ,注意到吃与被吃的关系是循环的,用点权表示该点与父亲节点的关系,路径压缩时用每个点到根的权值和模 \(3\) 作为该点的新权值。
倍增
倍增是一个大块,但是我觉得比起数据结构来说它更像是一种思想。
倍增地求,倍增的一维往往表示“走 \(2^i\) 步”或者“一直到 \(2^i\) 个点后”,倍增的查询一种是参考快速幂的直接二进制分解,另一种则是参考倍增求 \(LCA\) 的“不满足某种性质的最后的点”。倍增数组的处理也不一定就是 \(O(1)\) 转移,有时可以配合线段树在增加了一个 \(\log\) 的情况下处理倍增数组。
相对于其它数据结构,倍增更重要的当然是倍增的思想,不同的题目的倍增维护的信息不同,思想也是不同的,这里给出更多的例题。
例题 \(P1226\) ,快速幂。
例题 \(P3379\) ,倍增求 \(LCA\) 。
例题 \(P1081\) ,经典倍增题,将小 \(A\) 与小 \(B\) 各驾驶一天做为一个整体,预处理,维护两人各行驶的路程,进行倍增。
例题 \(P1084\) ,二分+倍增,二分一个时间,倍增每个军队可以走到的最高点,若军队能走到根就存下剩余时间,将空闲军队放到未完全防住的城市。
例题 \(P3390\) ,矩阵快速幂。注意到最短路中三角不等式形式为 \(dis_{a,b}=\min \{ dis_{a,c}+dis_{c,b}\}\) ,可以将路径信息转化为 \(min-plus\) 矩阵,将 \(floyd\) 的过程转化为 \(min-plus\) 矩阵乘法,从而在 \(O(n^3\log x)\) 的时间内维护路径边数小于等于/等于 \(x\) 的最短路。维护路径可行性同理。
ST表
ST 表是用于解决 可重复贡献问题 的数据结构。
区间最值与 \(\gcd\) 运算、按位或都是 可重复贡献问题 。所以ST表可用于解决这些问题。
ST表基于倍增的思想,对于一个静态的数组,ST表预处理出从 \(i\) 开始,长度为 \(2^j\) 的区间内的答案,例如区间最小值的ST表有:
ST表的预处理如上是 \(\Theta(n\log n)\) 的,而查询则是 \(\Theta(1)\) 的。由于ST表维护的问题贡献可重复,所以可以直接在查询区间的头尾各取出一个长为 $2^\left \lfloor \log_2{(r-l+1)} \right \rfloor $ 的区间直接可重复地计算贡献。
ST表的优势完全在于它在可重复贡献问题上的快速查询。事实上,ST表也可以 \(\log\) 地查询不可重复贡献问题。但是如果这样,我为什么不用线段树呢。
例题 \(P2866\) ,二分能看到的右端点使区间内数值都小于自身,使用ST表求 \(RMQ\) 问题。