题目描述
定义完美序列:若一个序列内没有重复的数,称这个数列为完美数列。
每次给定一个区间 \([l,r]\),求这个区间内最长的完美序列长度。
具体思路
设 \(len_i\) 表示从 \(i\) 出发往右的最长完美序列长度。
我们定义一个指针 \(st\),表示当前枚举的区间左端点,同时定义多一个指针 \(now\),表示当前枚举到了哪个点。
我们还要用一个 \(last\) 数组记录每个数上一次出现的位置。
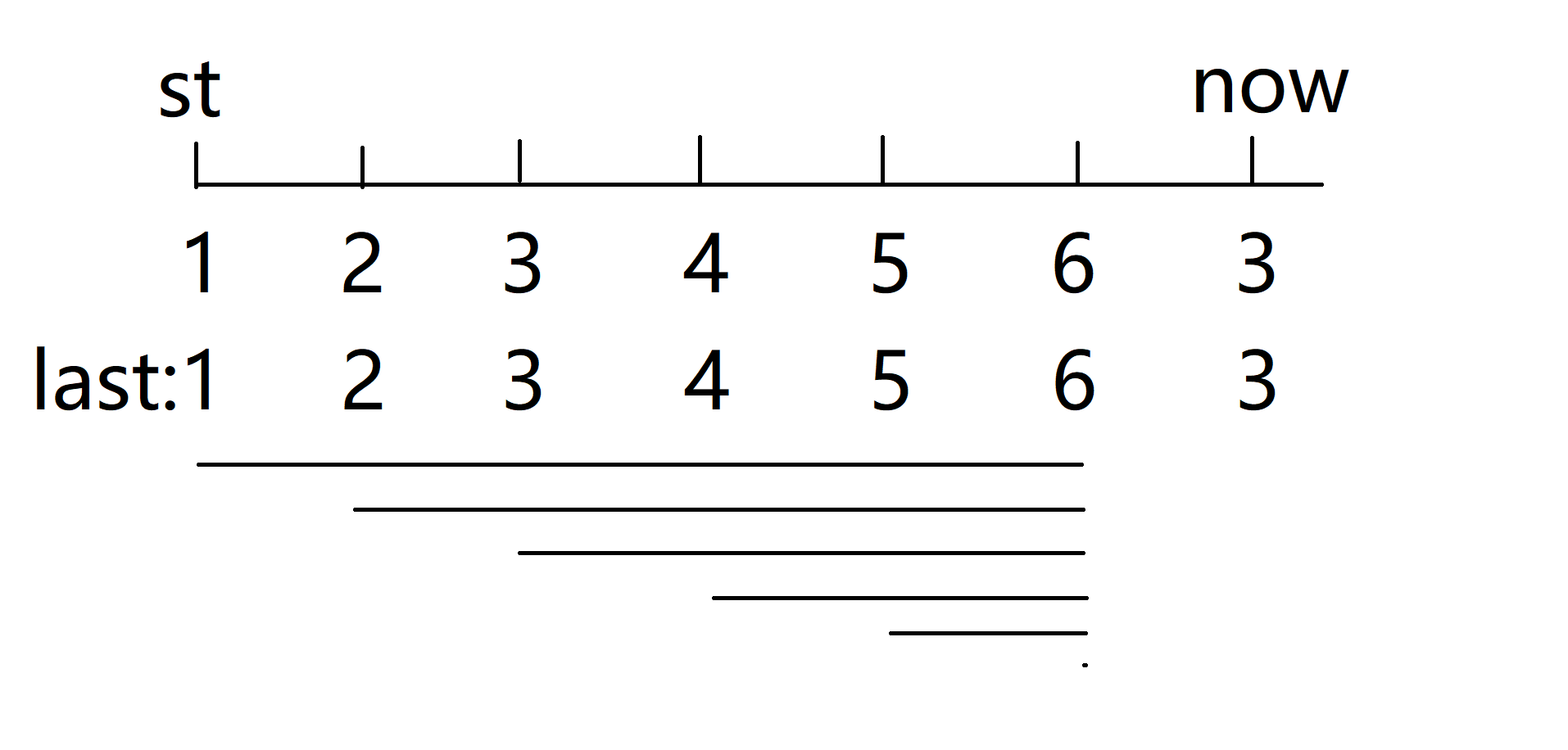
如图所示,如果当前的数 \(a[now]\) 上一次出现的位置在 \(st\) 之后,说明 \(a[now]\) 是这段区间内第一个重复的,同时也说明 \(now\) 前面这段区间是没有重复的。
那么以 \(st \sim now-1\) 这段区间的点为起点的最长完美序列的右端点都是 \(now-1\)。
那我们就可以更新这一段的信息,同时将 \(st\) 指针指向 \(now\) 指针所处位置,并进行下一轮枚举。
这样我们就实现了 \(O(n)\) 处理出 \(len_i\) 的值。
接下来考虑区间查询。
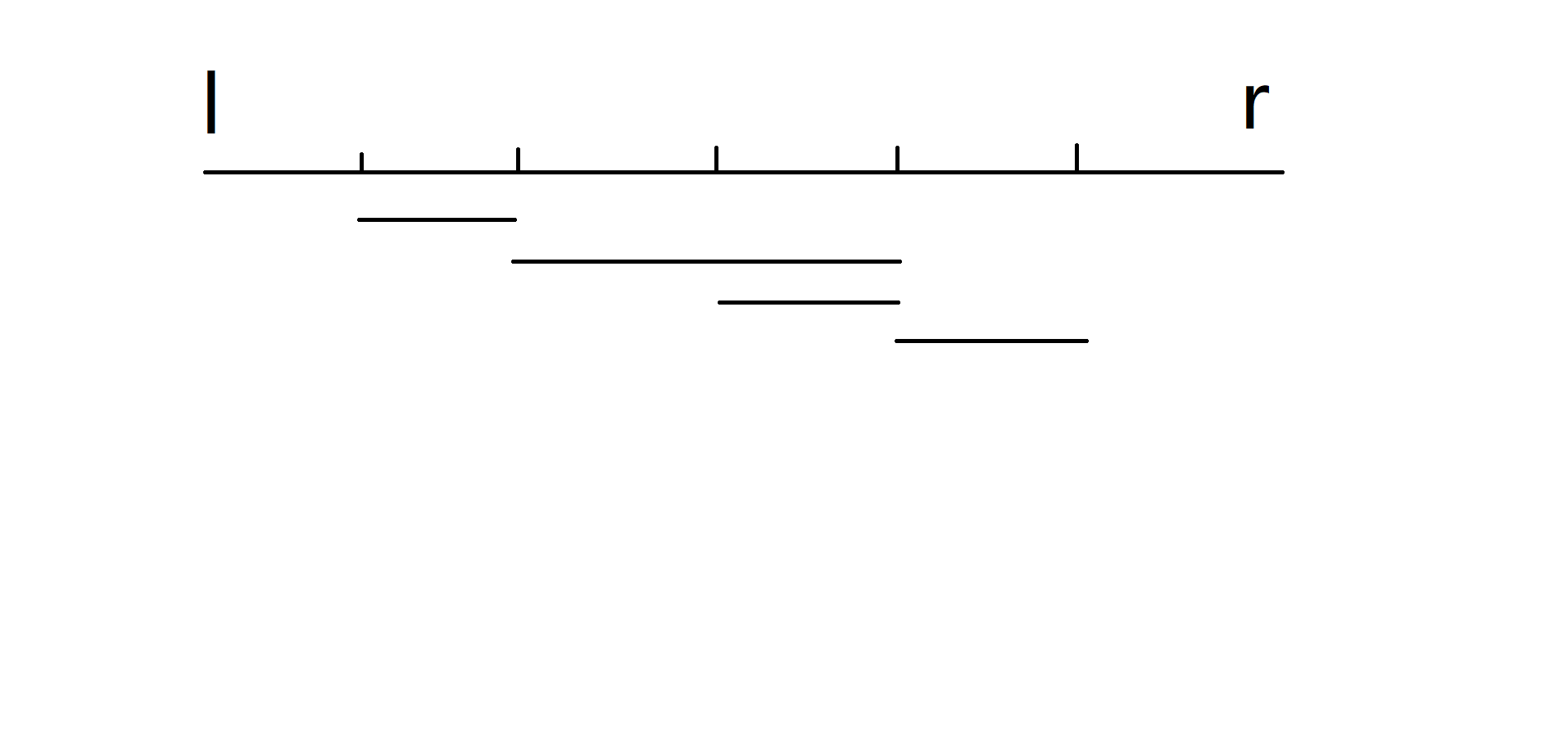
如图所示,以 \(l \sim r\) 区间内的点为起点的最长完美序列的右端点都没有超过 \(r\),那么我们直接对 \(len_i\) 取最大值即可。
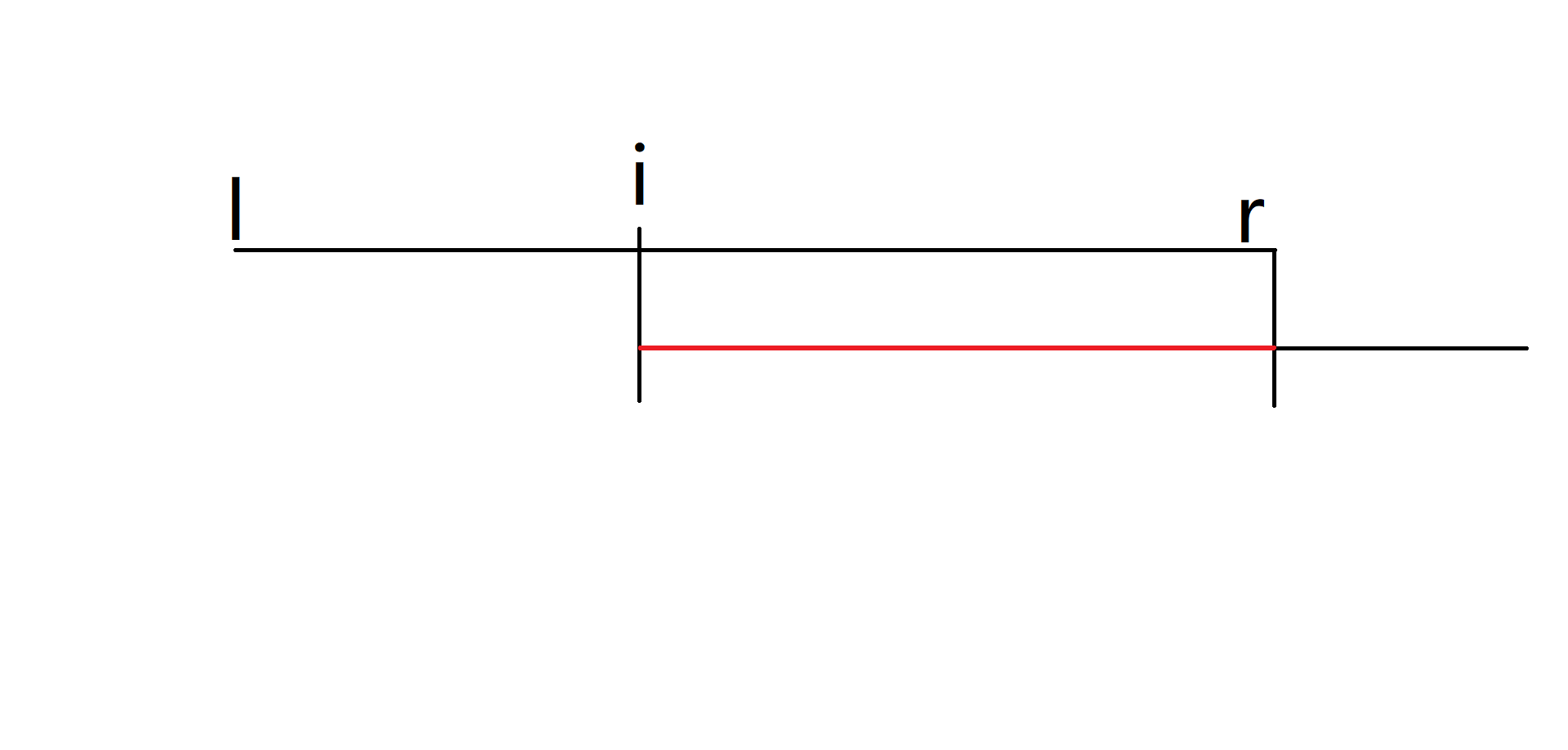
但是有可能有这种情况, 以 \(l \sim r\) 区间内的点为起点的最长完美序列的右端点超过 \(r\) 了,这个时候超过 \(r\) 的部分我们就不能要了。
那么我们就有暴力代码 \(1\):
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5,M=1e6+5;
int ed[N],last[2*M+5],a[N],len[N];
int main(){
int n,m;scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
a[i]=a[i]+M;
}
int st=1,now=2;
last[a[1]]=1;
while(now<=n){
if(last[a[now]]>=st){
int pos=last[a[now]];
for(int i=st;i<=pos;i++){
ed[i]=now-1;
len[i]=now-1-i+1;
last[a[i]]=0;
}
st=pos+1;
}
last[a[now]]=now;
now++;
}
for(int i=st;i<=n;i++){
ed[i]=n;
len[i]=n-i+1;
}
for(int i=1;i<=m;i++){
int l,r;scanf("%d%d",&l,&r);
l++,r++;
int ans=0;
for(int j=l;j<=r;j++){
if(ed[j]>r){
ans=max(ans,r-j+1);
}
else{
ans=max(ans,len[j]);
}
}
printf("%d\n",ans);
}
return 0;
}
我们继续分析性质。
我们发现如果区间内有一个点 \(i\),以它为起点的最长完美序列的右端点超过了 \(r\),那么 \(i+1 \sim r\) 这一段区间内的点一定被包含在这段完美序列内,我们就不需要继续往后找了。
于是有暴力代码 \(2\):
#include<bits/stdc++.h>
#pragma GCC optimize("Ofast")
using namespace std;
const int N=2e5+5,M=1e6+5;
int ed[N],last[2*M+5],a[N],len[N];
int main(){
int n,m;scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
a[i]=a[i]+M;
}
int st=1,now=2;
last[a[1]]=1;
while(now<=n){
if(last[a[now]]>=st){
int pos=last[a[now]];
for(int i=st;i<=pos;i++){
ed[i]=now-1;
len[i]=now-1-i+1;
last[a[i]]=0;
}
st=pos+1;
}
last[a[now]]=now;
now++;
}
for(int i=st;i<=n;i++){
ed[i]=n;
len[i]=n-i+1;
}
for(int i=1;i<=m;i++){
int l,r;scanf("%d%d",&l,&r);
l++,r++;
int ans=0;
for(int j=l;j<=r;j++){
if(ed[j]>r){
if(r-j+1>ans){
ans=r-j+1;
break;
}
}
else{
ans=max(ans,len[j]);
}
}
printf("%d\n",ans);
}
return 0;
}
这个时候我们可以将询问离线操作,将右端点按升序排序。
我们定义一个 \(now\) 指针,是用来找到 \([l,r]\) 区间内第一个最长完美序列右端点大于等于 \(r\) 的点。
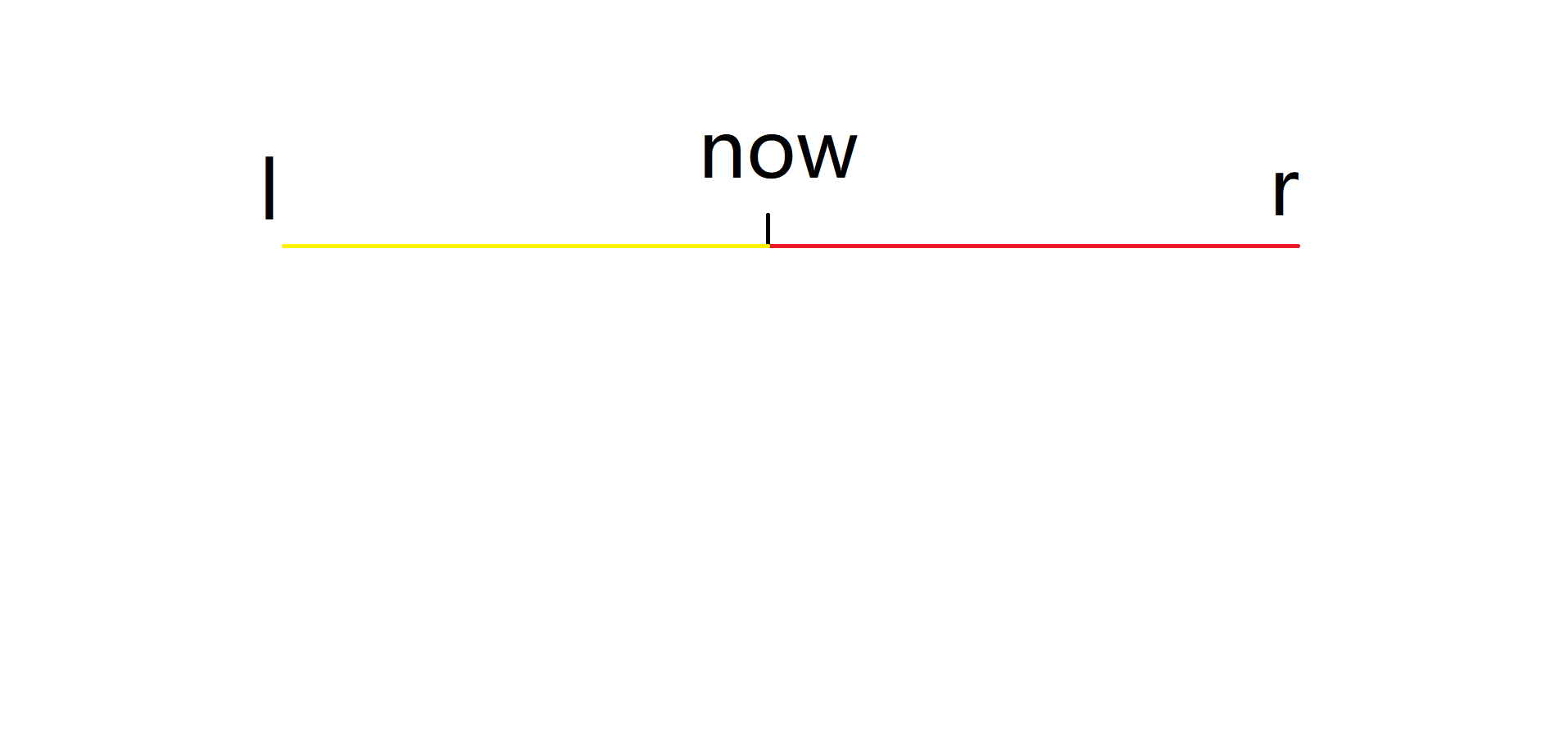
- 对于 \(now \sim r\) 这段区间,即上图中的红色线段。贡献为 \(r-now+1\)。
- 对于 \(l \sim now-1\) 这段区间,即上图中的黄色线段,由于它们最长完美序列右端点不超过 \(r\),我们就可以用第一份暴力代码的方式来求 \(l \sim now-1\) 这段区间 \(len_i\) 的最大值,我们可以用 st 表或者线段树来维护。
由于我们将区间右端点排好了序,因此每次的 \(now\) 指针只需要继承上一次的即可,就不用每次都重新枚举了。
时间复杂度:\(O(n \log n)\)。
Code
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5,M=1e6;
struct node{
int l,r,id;
}q[N];
bool cmp(node n1,node n2){
return n1.r<n2.r;
}
int ans[N];
int last[2*M+5],a[N],len[N];
int n,m,f[N][26],mylog[N];
void build(){
for(int i=1;i<=n;i++){
mylog[i]=log2(i);
}
for(int i=1;i<=n;i++){
f[i][0]=len[i];
}
for(int j=1;j<=25;j++){
for(int i=1;i+(1<<j)-1<=n;i++){
f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}
}
}
int query(int l,int r){
int k=mylog[r-l+1];
return max(f[l][k],f[r-(1<<k)+1][k]);
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
a[i]=a[i]+M;
}
int st=1,now=2;
last[a[1]]=1;
while(now<=n){
if(last[a[now]]>=st){
int pos=last[a[now]];
for(int i=st;i<=pos;i++){
len[i]=now-1-i+1;
last[a[i]]=0;
}
st=pos+1;
}
last[a[now]]=now;
now++;
}
for(int i=st;i<=n;i++){
len[i]=n-i+1;
}
build();
for(int i=1;i<=m;i++){
scanf("%d%d",&q[i].l,&q[i].r);
q[i].l++,q[i].r++;
q[i].id=i;
}
sort(q+1,q+m+1,cmp);
now=1;
for(int i=1;i<=m;i++){
while(now+len[now]-1<q[i].r)now++;
if(now<=q[i].l)ans[q[i].id]=q[i].r-q[i].l+1;
else{
ans[q[i].id]=max(q[i].r-now+1,query(q[i].l,now-1));
}
}
for(int i=1;i<=m;i++){
printf("%d\n",ans[i]);
}
return 0;
}