第五章 树及二叉树
书面作业
来源:算法与数据结构复习 第五章 树及二叉树(详解)_二叉树的中序遍历也可以循环地完成。给定循环中堆栈的操作序列如下(其中push为入-CSDN博客
一、判断题
1、某二叉树的前序和中序遍历序列正好一样,则该二叉树中的任何结点一定都无左孩子。 (T)
解析:
二叉树的前序是先根再左再右,中序是先左再根再右;若相同,则没有左;
2、若一个结点是某二叉树的中序遍历序列的最后一个结点,则它必是该树的前序遍历序列中的最后一个结点。(F)
解析:
中序遍历序列的最后一个结点可能是根或右子树,而前序遍历的最后一个结点可能是左子树和根;
举反例:
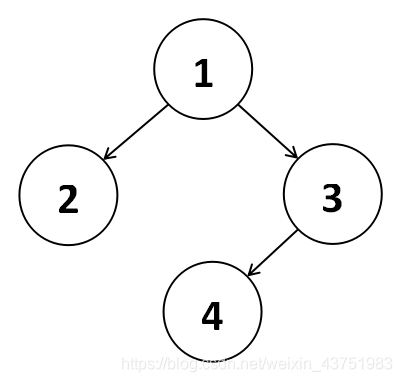
前序遍历:1 2 3 4
中序遍历:2 1 4 3
3、将一棵完全二叉树存于数组中(根结点的下标为 1)。则下标为 23 和 24 的两个结点是兄弟。(F)
解析:
方法一:(利用完全二叉树的性质)
对于n个结点的完全二叉树tree,有如下特点:
(1)若i为奇数且i>1,那么tree的左兄弟为tree[i-1];
(2)若i为偶数且i<n,那么tree的右兄弟为tree[i+1];
(3)若i>1,tree的父亲节点为tree[i div 2];(div:整除)
(4)若2 * i<=n,那么tree的左孩子为tree[2 * i];若2 * i+1<=n,那么tree的右孩子为tree[2 * i+1];
(5)若i>(n div 2),那么tree[i]为叶子结点(对应(3));
(6)若i<((n-1) div 2),那么tree[i]必有两个孩子(对应(4));
由(1)(2)可知:23为奇数,且23>1,23的左兄弟为22;
方法二:画图
4、对 N(≥2)个权值均不相同的字符构造哈夫曼树,则树中任一非叶结点的权值一定不小于下一层任一结点的权值。(T)
解析:
当用 n 个结点(都做叶子结点且都有各自的权值)试图构建一棵树时,如果构建的这棵树的带权路径长度最小,称这棵树为“最优二叉树”,有时也叫“赫夫曼树”或者“哈夫曼树”。
在构建哈弗曼树时,要使树的带权路径长度最小,只需要遵循一个原则,那就是:权重越大的结点离树根越近。
5、二叉树不是树的特殊情况。(T)
解析:
树和二叉树的2个主要差别:
- 树中结点的最大度数没有限制,而二叉树结点的最大度数为2;
- 树的结点无左、右之分,而二叉树的结点有左、右之分;
注意:尽管二叉树与树有许多相似之处,但二叉树不是树的特殊情形。
6、树的后根序遍历序列等同于它所对应二叉树的中序遍历序列。(T)
解析:
一棵树的后根遍历与这棵树所对应的二叉树的中序遍历相同。因为树转化为二叉树后是没有右子树的,所以最后访问的是树的根结点。
- 树转二叉树:
- 树中所有相同双亲结点的兄弟结点之间加一条连线;
- 对树中不是双亲结点的第一个孩子的结点,只保留新添加的该结点与左兄弟结点之间的连线,删去该结点与双亲结点之间的连线;
- 整理所有保留的连线,根据连线摆放成二叉树的结构,转换完成;
- 后根遍历过程:
- 按照从左到右的次序后根遍历根结点的每一棵子树;
- 访问根结点。
7、将一棵树转成二叉树,根结点没有左子树。(F)
解析:
由题6可知,没有右子树;
8、已知一棵二叉树的先序遍历结果是 ABC, 则 CAB 不可能是中序遍历结果。(T)
解析:
根据先序遍历结果,可知根结点是A,左孩子是B,右孩子是C,由此可知中序遍历的结果是BAC;
9、一棵有 124 个结点的完全二叉树,其叶结点个数是确定的。(T)
解析:
完全二叉树要按照从左到右,从上到下的规则插入元素,因此他的结构是唯一的,所以叶结点的个数是确定的;
10、对于一个有 N 个结点、K 条边的森林,不能确定它共有几棵树。(F)
解析:
设有M棵树,M={M1,M2,M3,M4…};
对于一棵树,有结论:边数=结点数-1,即v=n-1;
则有:
- N=n1+n2+n3+n4+…
- K=v1+v2+v3+v4+…=n1-1+n2-1+n3-1+n4-1+…=N-M
- M=N-K
N-K是定值,可确定;
11、二叉树通常有顺序存储结构和链式存储结构。(T)
12、设只包含根结点的二叉树高度为 0,则高度为 k 的二叉树最小结点数为 k+1。 (T)、
解析:
只有一条路径的二叉树;
13、二叉树是度为 2 的树。(F)
解析:
二叉树不是树;
14、二叉树可以用二叉链表存储,树无法用二叉链表存储。(F)
15、完全二叉树中,若一个结点没有左孩子,则它必是树叶。(T)
二、单选题
1、 按照二叉树的定义,具有 3 个结点的二叉树有几种? (C )
A. 3
B. 4
C. 5
D. 6
2、二叉树中第 5 层(根的层号为 1)上的结点个数最多为:(C )
A. 8
B. 15
C. 16
D. 32
解析:
第i层的结点数做多为:2 i − 1 2^{i-1}2i−1
3、在一个用数组表示的完全二叉树中,如果根结点下标为 1,那么下标为 17 和 19 这两个结点的最近公共祖先结点在哪里(数组下标)? (注:两个结点的“公共祖先结点”是指同时都是这两个结点祖先的结点) (B)
A. 8
B. 4
C. 2
D. 1
解析:
17的父节点为8,19的父节点为9,8和9的父节点为4;
4、设一段文本中包含 4 个对象{a,b,c,d},其出现次数相应为{4,2,5,1},则该段文本的哈夫曼编码比采用等长方式的编码节省了多少位数? (B)
A. 0
B. 2
C. 4
D. 5
解析:
Huffman树构造算法:
- 将 {ω1,ω2,…,ωn}{ω1,ω2,…,ωn}看成是有 n 棵树的森林(每棵树仅有一个节点)
- 在森林中选出两个根节点的权值最小的树合并,作为一个新树的左右子树,且新树的根节点权值为其左右子树根节点的权值之和
- 从森林中删除选取的两棵树,并将新树加入森林
- 重复步骤2、3,直到森林中只剩一棵树为止,该树即为所求的Huffman树。
普通编码:
a:00
b:01
c:10;
d:11;
长度:2*(4+2+5+1)=24;
哈夫曼编码:
011001d=1b=23a=4c=5712
a:01
b:001
c:1
d:000
长度:2 * 4 + 3 * 2 + 1 * 5 + 3 * 1 = 22;
24-22=2;
5、下列线索二叉树中(用虚线表示线索),符合后序线索树定义的是: (D)
解析:
- 若结点的左子树为空,则该结点的左孩子指针指向其前驱结点。
- 若结点的右子树为空,则该结点的右孩子指针指向其后继结点。
6、已知一棵完全二叉树的第 9 层(设根为第 1 层)有 100 个叶结点,则该完全二叉树的结点
个数最多是: (B)
A. 311
B. 823
C. 1847
D. 无法确定
解析:
个数=( 2 9 − 1 − 100 ) ∗ 2 + 2 9 − 1 = ( 256 − 100 ) ∗ 2 + 511 = 312 + 511 = 823 (2{9-1}-100)*2+29-1=(256-100)*2+511=312+511=823(29−1−100)∗2+29−1=(256−100)∗2+511=312+511=823
7、如果二叉树的前序遍历结果是 12345,后序遍历结果是 24531,那么该二叉树的中序遍历
结果是什么? ©
A. 23145
B. 32154
C. 21435
D. 无法确定
解析:
12345
8、二叉树的中序遍历也可以循环地完成。给定循环中堆栈的操作序列如下(其中 push 为入栈,pop 为出栈):push(1), push(2), push(3), pop(), push(4), pop(), pop(), push(5), pop(),pop(), push(6), pop()以下哪句是对的?(A)
A. 3 和 5 是兄弟结点
B. 1 是 5 的父结点
C. 6 是根结点
D. 以上全不对
解析:
二叉树实现如图
123456
9、下面的函数 PreOrderPrintLeaves(BinTree BT)按前序遍历的顺序打印出二叉树 BT 的所有叶子结点。则下列哪条表达式应被填在空中?(D)
void PreOrderPrintLeaves( BinTree BT ) {
if (BT) {
if (___________________)
printf(" %d", BT->Data);
PreOrderPrintLeaves( BT->Left );
PreOrderPrintLeaves( BT->Right );
}
}
12345678
A. BT->Data != 0
B. !BT->Right
C. !BT->Left
D. !(BT->Left || BT->Right)
10、树最适合于用来表示 (D)
A. 有序数据元素
B. 无序数据元素
C. 元素之间无联系的数据
D. 元素之间具有分支层次关系的数据
11、三叉树中,度为 1 的结点有 5 个,度为 2 的结点 3 个,度为 3 的结点 2 个,问该树含有几个叶结点? (A)
A. 8
B. 10
C. 12
D. 13
解析:
叶结点的度为0;
设叶结点的个数为X;
5 * 1 + 2 * 3 + 3 * 2 + X * 0 + 1(根节点)= 5 + 3 + 2 + X ;
解的X=8;
12、已知一棵二叉树的树形如下图所示,其后序序列为{ e, a, c, b, d, g, f }。树中与结点 a 同
层的结点是:(B)
A. c
B. d
C. f
D. g
解析:
由后续遍历可得,f是根结点;左子树和右子树的个数都为3,所以 e, a, c是左子树,b, d, g是右子树;
c是左子树的根结点,g是右子树的根节点;然后再分析可得出完整的二叉树;
如图:
fcgaedb
13、具有 65 个结点的完全二叉树其深度为(根的深度为 1): (B)
A. 8
B. 7
C. 6
D. 5
解析:
若完全二叉树为N层,则最多由2 n − 1 2^n-12n−1个结点;
2 6 − 1 < 65 < 2 7 − 1 26-1<65<27-126−1<65<27−1
深度为7;
14、已知字符集{ a, b, c, d, e, f, g, h }。若各字符的哈夫曼编码依次是 0100, 10, 0000, 0101, 001,
011, 11, 0001,则编码序列 0100011001001011110101 的译码结果是:(D)
A. acgabfh
B. adbagbb
C. afbeagd
D. afeefgd
15、对于一个有 N 个结点、K 条边的森林,共有几棵树? (A)
A. N−K
B. N−K+1
C. N−K−1
D. 不能确定
解析:
和判断题10类似;
16、任何一棵二叉树的叶结点在先序、中序和后序遍历序列中的相对次序 (B)
A. 发生改变
B. 不发生改变
C. 不能确定
D. 以上都不对
解析:
因为根据三个遍历的次序和特点:前序是根左右、中序是左根右、后序是左右根,因此相对次序发生变化的都是子树的根,也就是分支结点。
17、将森林转换为对应的二叉树,若在二叉树中,结点 u 是结点 v 的父结点的父结点,则在原来的森林中,u 和 v 可能具有的关系是: (B)
1 .父子关系; 2. 兄弟关系; 3. u 的父结点与 v 的父结点是兄弟关系
A. 只有 2
B. 1 和 2
C. 1 和 3
D. 1、2 和 3
18、已知字符集{ a, b, c, d, e, f },若各字符出现的次数分别为{ 6, 3, 8, 2, 10, 4 },则对应字符集
中各字符的哈夫曼编码可能是:(A)
A. 00, 1011, 01, 1010, 11, 100
B. 00, 100, 110, 000, 0010, 01
C. 10, 1011, 11, 0011, 00, 010
D. 0011, 10, 11, 0010, 01, 000
三、填空题
1、假设二叉树的存储结构为二叉链表,在具有 n 个结点的二叉链表中(n>0),左孩子指针域和右孩子指针域的个数为( 2n),空指针域的个数为 (n+1) 。
解析:
空指针域的个数为=2n-(n-1)=n+1;
2、在含有 n 个结点的树中,边数只能是 (n-1)。
3、如果二叉树的后序遍历结果是 FDEBGCA,中序遍历结果是 FDBEACG,那么该二叉树的前序遍历结果是: (ABDFECG)。
解析:
ABCDEGF
4、已知一棵完全二叉树的第 5 层(设根为第 1 层)有 8 个叶结点,则该完全二叉树的结点个数最多是: (47)
解析:
( 2 5 − 1 − 8 ) ∗ 2 + 2 5 − 1 = 47 (2^{5-1} -8)*2+2^5-1=47(25−1−8)∗2+25−1=47
完全二叉树:一棵深度为k的有n个结点的二叉树,对其结点按从上至下,从左至右的顺序进行编号,如果编号为i的结点与满二叉树中编号为i的结点在二叉树的位置相同,则这棵二叉树为完全二叉树。
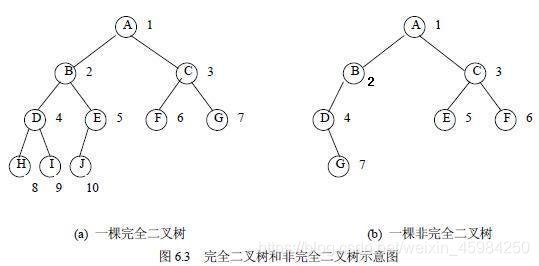
因为一棵非空二叉树的第i层上最多有 2的(i-1)次方个结点,所以可以推广到完全二叉树
性质1:一棵完全二叉树的第i层上最多有 2的(i-1) 次方个结点
因为一棵深度为k的二叉树中,最多有 2的k次方-1 个结点,也可以推广到完全二叉树
性质2:一棵深度为k的完全二叉树中,最多有 2的k次方-1 个结点
性质3:具有n个结点的完全二叉树的深度k为 log₂n向下取整,再+ 1。
例:有5个结点,log₂n向下取整为2,再+1为3。
由性质3可得,log₂124 向下取整 =6,再+1为7。
所以该二叉树的深度为7。
由性质2可得,深度为6的完全二叉树有2的6次方-1个结点,即63个结点。
总共有124个结点,那么还剩下124-63=61个结点,分布在第7层。
由性质1可得,第7层最多有2的(i-1)次方个结点,也就是2的6次方,最多64个,可以容纳下61个结点。
下面计算叶结点,第7层的结点全是叶节点,有61个,剩下的叶节点在第6层。
第7层的每2个结点是第6层的1个结点的左右孩子,因为61是奇数,所以最后还剩下一个结点对应第6层的一个结点。
(61-1)/2=30,即第6层有30个结点有左右孩子,有1个结点有1个孩子,第六层有2的5次方个结点,也就是32个,那么第6层没有孩子的结点有32-30-1=1个,这个结点是叶节点之一。
所以该完全二叉树共有61+1=62个叶节点
2.二叉树中序线索化后,不存在空指针域。 F
(无特殊说明的话,是没有头结点的,如果有头结点的话,为T)
第一个结点无前驱,最后一个结点无后继。
构造一个二叉树就偷点懒,用这个的结果(这叫复习/doge):
4-14 还原二叉树&&4-15 根据后序和中序遍历输出先序遍历
生成的树:
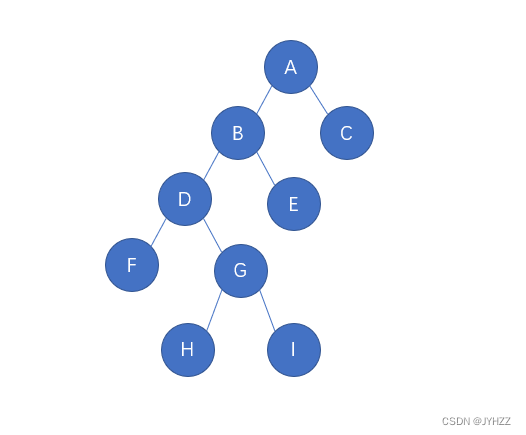
咱们就中序线索化这个。
代码:(有头结点的中序线索二叉树,不存在空指针域)
#include<iostream>
using namespace std;
typedef struct Tnode* Tree;
typedef struct Tnode{
char data;
Tree lchild;
Tree rchild;
unsigned ltag;
unsigned rtag;
};
Tree get(char s1[], char s2[], int n) {
if (n <= 0) {
return NULL;
}
Tree tree = (Tree)malloc(sizeof(struct Tnode));
tree->lchild = NULL;
tree->rchild = NULL;
tree->ltag = 0;
tree->rtag = 0;
tree->data = s1[0];
int i;
for (i = 0; s2[i] != s1[0]; i++);
tree->lchild = get(s1+1, s2, i);
tree->rchild = get(s1 + i + 1, s2 + i + 1, n - i - 1);
return tree;
}
int len(Tree tree) {
if (tree == NULL) {
return 0;
}
int left = len(tree->lchild);
int right = len(tree->rchild);
return (left >= right ? left : right) + 1;
}
Tree pre;
void InTreading(Tree tree) {
if (tree) {
InTreading(tree->lchild);
if (tree->lchild == NULL) {
tree->ltag = 1;
tree->lchild = pre;
}
if (pre->rchild == NULL) {
pre->rtag = 1;
pre->rchild = tree;
}
pre = tree;
InTreading(tree->rchild);
}
}
Tree InOrderThr(Tree tree) {
Tree head = (Tree)malloc(sizeof(struct Tnode));
head->lchild = 0;
head->rtag = 1;
head->rchild = head;
if (!tree) {
head->lchild = head;
}
else {
head->lchild = tree;
pre = head;
InTreading(tree);
pre->rchild = head;
pre->rtag = 1;
head->rchild = pre;
}
return head;
}
Tree InpostNode(Tree p) {
Tree post;
post = p->rchild;
if (p->rtag != 1) {
while (post->ltag == 0) {
post = post->lchild;
}
}
return post;
}
void Search(Tree tree) {
Tree temp;
temp = tree->lchild;
while (temp->ltag == 0 && temp != tree) {
temp = temp->lchild;
}
while(temp!=tree){
printf("%c ", temp->data);
temp = InpostNode(temp);
}
}
int main()
{
int n;
cin >> n;
char s1[51], s2[51];
for (int i = 0; i < n; i++) {
cin >> s1[i];
}
for (int i = 0; i < n; i++) {
cin >> s2[i];
}
Tree st= get(s1, s2, n);
st = InOrderThr(st);
Search(st);
return 0;
}
3.对N(≥2)个权值均不相同的字符构造哈夫曼树,则树中任一非叶结点的权值一定不小于下一层任一结点的权值。T
解析:考察哈弗曼树的构造方法,哈弗曼树的构造思想就是贪心的思想,每次选择权值最小的两个节点来形成新的节点,自底向上建树,因此对于一棵哈弗曼树来说,树中任一非叶节点的权值一定不小于下一层的任意节点的权值。
在构造哈夫曼树时会遇到两种情况,一种是造成树的高度增加,一种是不增加:
高度增加的情况:1,2,3,4。即每向树增加结点,树高加一
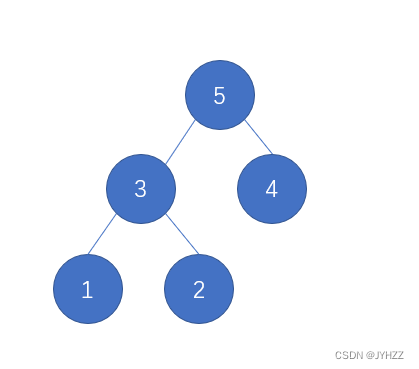
高度不增加的情况:比如6,7,8,9。在增加8和9时,树高不会立刻增加(就当成是树吧)
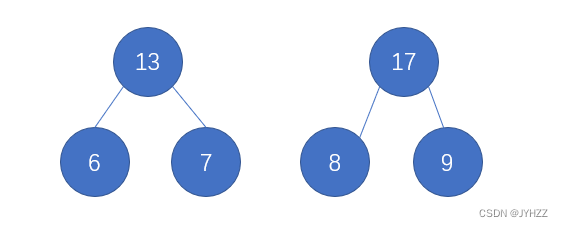
无论是这两种那种情况,都满足题意
4.哈夫曼编码是一种最优的前缀码。对一个给定的字符集及其字符频率,其哈夫曼编码不一定是唯一的,但是每个字符的哈夫曼码的长度一定是唯一的。F
哈夫曼编码一般左0右1
比如这个哈夫曼树:
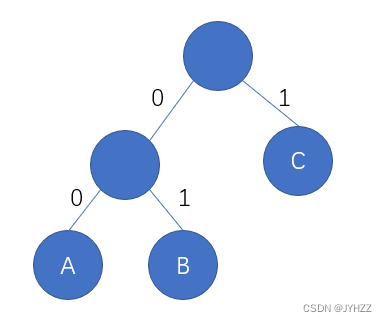
哈夫曼编码:
A:00
B:01
C:1
我们在构造时也可能会这样:
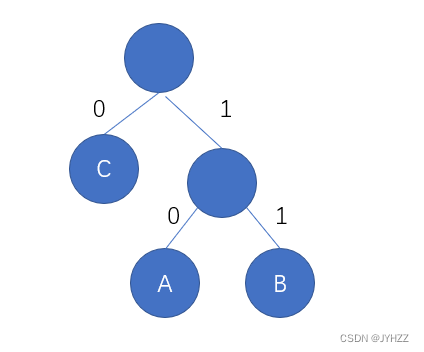
这样构造也是对的,但是哈夫曼编码就不一样了:
哈夫曼编码:
A:10
B:11
C:0
所以,对一个给定的字符集及其字符频率,哈夫曼编码不一定是唯一的。
因为可能有这种情况:字符集A,B,C,D出现的次数为1,2,2,2。这种情况每个字符的哈夫曼码的长度*不一定*是唯一的
5.对于一个有N个结点、K条边的森林,不能确定它共有几棵树。F
对于一棵树,有这样的性质:节点数-边数=1。
例如:
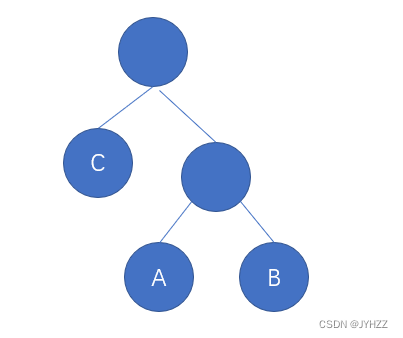
有5个结点,4条边
森林是0棵或有限棵不相交的树的集合,比如森林中有3棵树,那么每棵树的结点数比边数多1,那么三棵树的总结点数就比总边数多3。由此可得,对于一个有N个结点、K条边的森林,它有N-K棵树
6.树的后根序遍历序列等同于它所对应二叉树的中序遍历序列。T
树的先序遍历与其转换成二叉树的先序遍历的结果相同;
树的后序遍历与其转换成二叉树的中序遍历的结果相同;
7.二叉树可以用二叉链表存储,树无法用二叉链表存储。F
一个结点的第一个孩子(长子)作为该节点的左孩子,这个结点的兄弟这个结点作为右孩子。
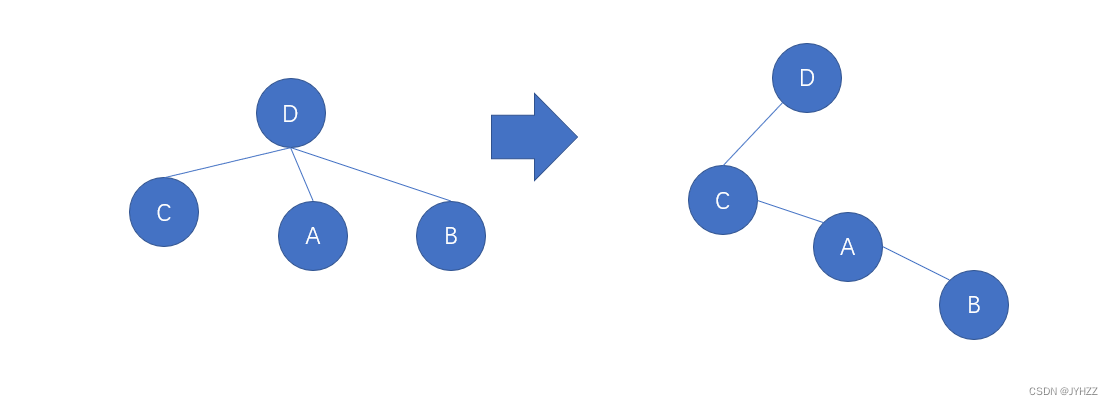
8.将一棵树转成二叉树,根结点没有左子树。F
根节点没有兄弟,所以根节点没有右子树
9.用邻接矩阵法存储图,占用的存储空间数只与图中结点个数有关,而与边数无关。T
占用的存储空间数只与图中结点个数有关,而与边数无关,空间代价为O(n*n);
10.用一维数组G[]存储有4个顶点的无向图如下:
G[] =
则顶点2和顶点0之间是有边的。T
下三角矩阵