矩阵求导与矩阵微分

简介

下面的 系列文章 来自知乎用户 iterator，是我见过最好的矩阵求导教程，没有之一！强烈推荐去看作者原文！

• 矩阵求导的本质与分子布局、分母布局的本质（矩阵求导——本质篇） - 知乎
• 矩阵求导公式的数学推导（矩阵求导——基础篇） - 知乎
• 矩阵求导公式的数学推导（矩阵求导——进阶篇） - 知乎
• 对称矩阵的求导，以多元正态分布的极大似然估计为例（矩阵求导——补充篇） - 知乎
• Matrix Calculus

分子布局和分母布局

具体讨论

向量变元实标量函数的分子布局偏导又称行向量偏导、行偏导向量
\(\text{D}_{\pmb{x}}f(\pmb{x})= \frac{\partial f(\pmb{x})}{\partial \pmb{x}^T}= \left[ \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \cdots, \frac{\partial f}{\partial x_n} \right]\)

向量变元实标量函数的分母布局偏导又称梯度向量、列向量偏导、列偏导向量
\(\nabla_{\pmb{x}}f(\pmb{x})= \frac{\partial f(\pmb{x})}{\partial \pmb{x}}= \left[ \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \cdots, \frac{\partial f}{\partial x_n} \right]^T\)

矩阵变元实标量函数的分子布局有 2 种形式
a. 将矩阵变元向量化并转置后求偏导的形式称为行向量偏导形式、行偏导向量形式
\(\begin{align*} \text{D}_{\text{vec}\pmb{X}}f(\pmb{X})&= \frac{\partial f(\pmb{X})}{\partial \text{vec}^T(\pmb{X})} \\\\ &= \left[ \frac{\partial f}{\partial x_{11}},\frac{\partial f}{\partial x_{21}},\cdots,\frac{\partial f}{\partial x_{m1}},\frac{\partial f}{\partial x_{12}},\frac{\partial f}{\partial x_{22}},\cdots,\frac{\partial f}{\partial x_{m2}},\cdots,\frac{\partial f} {\partial x_{1n}},\frac{\partial f}{\partial x_{2n}},\cdots,\frac{\partial f}{\partial x_{mn}} \right] \end{align*}\)

b. 将矩阵变元转置之后求偏导的形式称为 Jacobian 矩阵形式
\(\begin{align*} \text{D}_{\pmb{X}}f(\pmb{X})&= \frac{\partial f(\pmb{X})}{\partial \pmb{X}^T_{m\times n}} \\\\ &= \left[ \matrix{ \frac{\partial f}{\partial x_{11}}&\frac{\partial f}{\partial x_{21}}&\cdots&\frac{\partial f}{\partial x_{m1}} \\ \frac{\partial f}{\partial x_{12}}&\frac{\partial f}{\partial x_{22}}& \cdots & \frac{\partial f}{\partial x_{m2}}\\ \vdots&\vdots&\vdots&\vdots\\ \frac{\partial f} {\partial x_{1n}}&\frac{\partial f}{\partial x_{2n}}&\cdots&\frac{\partial f}{\partial x_{mn}} } \right]_{n\times m} \end{align*}\)

矩阵变元实标量函数的分母布局有 2 种形式
a. 将矩阵变元向量化后求偏导的形式称为梯度向量形式、列向量偏导形式、列偏导向量形式
\(\begin{align*} \nabla_{\text{vec}\pmb{X}}f(\pmb{X})&= \frac{\partial f(\pmb{X})}{\partial \text{vec}\pmb{X}} \\\\ &= \left[ \frac{\partial f}{\partial x_{11}},\frac{\partial f}{\partial x_{21}},\cdots,\frac{\partial f}{\partial x_{m1}},\frac{\partial f}{\partial x_{12}},\frac{\partial f}{\partial x_{22}},\cdots,\frac{\partial f}{\partial x_{m2}},\cdots,\frac{\partial f} {\partial x_{1n}},\frac{\partial f}{\partial x_{2n}},\cdots,\frac{\partial f}{\partial x_{mn}} \right]^T \end{align*}\)

b. 对矩阵变元直接求偏导的形式称为梯度矩阵形式
\(\begin{align*} \nabla_{\pmb{X}}f(\pmb{X})&= \frac{\partial f(\pmb{X})}{\partial \pmb{X}_{m\times n}} \\\\ &= \left[ \matrix{ \frac{\partial f}{\partial x_{11}}&\frac{\partial f}{\partial x_{12}}&\cdots&\frac{\partial f}{\partial x_{1n}} \\ \frac{\partial f}{\partial x_{21}}&\frac{\partial f}{\partial x_{22}}& \cdots & \frac{\partial f}{\partial x_{2n}}\\ \vdots&\vdots&\vdots&\vdots\\ \frac{\partial f} {\partial x_{m1}}&\frac{\partial f}{\partial x_{m2}}&\cdots&\frac{\partial f}{\partial x_{mn}} } \right]_{m\times n} \end{align*}\)

\(\text{vec}({\pmb{X})}= \left[x_{11},x_{21},\cdots,x_{m1},x_{12},x_{22},\cdots,x_{m2},\cdots,x_{1n},x_{2n},\cdots,x_{mn} \right]^T\) 表示把一个矩阵拉成列向量，即从第一列到最后一列依次堆起来。

分析总结

首先需要有个概念，就是分子布局和分母布局并非两个完全不相容的标记系统，二者本质上只是差了一个转置，所以可以把二者的关系统一的看，就是一个矩阵和它的转置的关系，应用中也可能同时出现，并可以互相转换。

其次，如何区分分子布局和分母布局，简单来说“分子和分母，谁没有被转置，就是谁的布局”，具体的可能如下：

在符号表示中，除非特别说明，我们一般认为，\(x\) 表示一个标量， \(\mathbf{x}\) 表示一个列向量，它的转置 \(\mathbf{x}^T\) 是行向量；\(\mathbf{X}\) 表示矩阵。

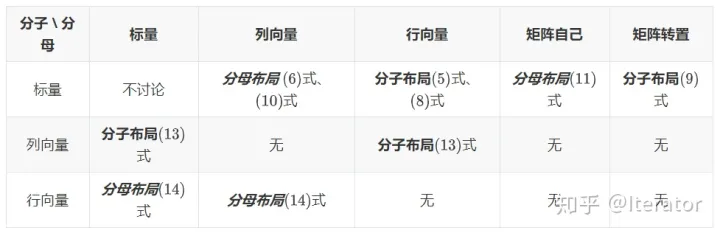
分子布局和分母布局的本质

• 分子布局：分子是标量、列向量、矩阵向量化后的列向量；分母是标量、列向量转置后的行向量、矩阵的转置矩阵、矩阵向量化后的列向量转置后的行向量。
• 分母布局：分子是标量、列向量转置后的行向量、矩阵向量化后的列向量转置后的行向量；分母是标量、列向量、矩阵自己、矩阵向量化后的列向量。
• 同类型的分子布局和分母布局结果一般是转置关系

矩阵导数

基本法则

常数求导
与一元函数常数求导相同：结果为零向量/矩阵

其中， \(c\) 为常数。

线性法则
与一元函数求导线性法则相同：相加再求导等于求导再相加，常数提外面

乘积法则
与一元函数求导乘积法则相同：前导后不导 加 前不导后导

商法则
与一元函数求导商法则相同：（上导下不导 减 上不导下导）除以（下的平方）

常用公式

向量变元的实值标量函数

\(\frac{\partial( \pmb{x}^T \pmb{a})}{\partial{\pmb{x}}} = \frac{\partial( \pmb{a}^T\pmb{x})}{\partial{\pmb{x}}} = \pmb{a} \\\\ \tag{9}\)

其中，\(\pmb{a}\) 为常数向量， \(\pmb{a}=(a\_1,a\_2,\cdots,a\_n)^T\) 。

\(\frac{\partial( \pmb{a}^T\pmb{X}^T\pmb{b})}{\partial{\pmb{X}}} = \pmb{b}\pmb{a}^T\)

其中， \(\pmb{a}_{n \times 1},\pmb{b}_{m \times 1}\) 为常数向量，\(\pmb{a}\_=(a_1,a_2,\cdots,a\_n)^T,\pmb{b}=(b_1,b_2,\cdots,b_m)^T\)。

\(\frac{\partial( \pmb{a}^T\pmb{X}\pmb{X}^T\pmb{b})}{\partial{\pmb{X}}} = \pmb{a}\pmb{b}^T\pmb{X}+\pmb{b}\pmb{a}^T\pmb{X}\)

其中， \(\pmb{a}_{m \times 1},\pmb{b}_{m \times 1}\) 为常数向量，\(\pmb{a}_=(a_1,a_2,\cdots,a_m)^T,\pmb{b}=(b_1,b_2,\cdots,b_m)^T\)。

\(\frac{\partial( \pmb{a}^T\pmb{X}^T\pmb{X}\pmb{b})}{\partial{\pmb{X}}} = \pmb{X}\pmb{b}\pmb{a}^T+\pmb{X}\pmb{a}\pmb{b}^T \\\\ \tag{33}\)

其中， \(\pmb{a}_{n \times 1},\pmb{b}_{n \times 1}\) 为常数向量，\(\pmb{a}_=(a_1,a_2,\cdots,a_n)^T,\pmb{b}=(b_1,b_2,\cdots,b_n)^T\)。

矩阵变元的实值标量函数

其中， \(\pmb{a}_{m \times 1}\),\(\pmb{b}_{n \times 1}\) 为常数向量，\(\pmb{a}_=(a_1,a_2,\cdots,a_m)^T,\pmb{b}=(b_1,b_2,\cdots,b_n)^T\)

其中， \(\pmb{a}_{n \times 1}\),\(\pmb{b}_{m \times 1}\) 为常数向量，\(\pmb{a}_=(a_1,a_2,\cdots,a_n)^T,\pmb{b}=(b_1,b_2,\cdots,b_m)^T\)

其中， \(\pmb{a}_{m \times 1}\),\(\pmb{b}_{m \times 1}\) 为常数向量，\(\pmb{a}_=(a_1,a_2,\cdots,a_m)^T\),\(\pmb{b}=(b_1,b_2,\cdots,b_m)^T\)。

其中， \(\pmb{a}_{n \times 1}\),\(\pmb{b}_{n \times 1}\) 为常数向量，\(\pmb{a}_=(a_1,a_2,\cdots,a_n)^T\),\(\pmb{b}=(b_1,b_2,\cdots,b_n)^T\)。

矩阵微分与矩阵求导

矩阵微分很大的一个用处就是去推导矩阵的导数，从而不用死记硬背上面这些导数的结果

矩阵的迹

定义

\(n \times n\) 的方阵 \(\pmb{A}_{n \times n}\) 的主对角线元素之和就叫矩阵 \(\pmb{A}\) 的迹 (trace)，记作 \(\mathbb{tr}(\pmb{A})\) ，即：

\(\pmb{A}\) 的迹为：

注意：只有方阵才有迹。

性质

标量的迹

对于一个标量 \(x\) ,可以看成是 \(1 \times 1\) 的矩阵，它的迹就是它自己。

线性法则

相加再求迹等于求迹再相加，标量提外面

其中， \(c_1,c_2\) 为标量。

乘积的迹及其本质

对于两个阶数都是 \(m \times n\) 的矩阵 \(\pmb{A}_{m\times n},\pmb{B}_{m\times n},\), 其中一个矩阵乘以（左乘右乘都可以）另一个矩阵的转置的迹，本质是 \(\pmb{A}_{m\times n},\pmb{B}_{m\times n}\) 两个矩阵对应位置的元素相乘并相加，可以理解为向量的点积在矩阵上的推广，即：

转置法则

转置的迹等于原矩阵的迹

交换律

矩阵乘积位置互换，迹不变

其中， \(\pmb{A}_{m \times n},\pmb{B}_{n \times m}\) 。交换律可以进一步推广到多个矩阵相乘的场景下，即

其中， \(\pmb{A}_{m \times n},\pmb{B}_{n \times p},\pmb{C}_{p \times m}\)。

熟练使用

其中， \(\pmb{A}_{m \times n},\pmb{B}_{m \times n}\) 。
第一个和第二个是交换律，第二个和三个是转置，第三个和第四个是交换律。

标量变元函数的微分

一元函数的微分

普通函数的微分

设 \(y=f(x)\) ， \(y\) 可导，则其微分为：

复合函数的微分
设 \(y=f(u),u=g(x)\)，均可导，则 \(y\) 的微分为：

多元函数的全微分

普通函数的全微分

设 z=f(x,y) ， z 可微，则其全微分为：

复合函数的全微分

设 \(z=f(u),u=\varphi(x,y)\) , \(z\) 可导， \(u\) 可微，则其全微分为：

微分/全微分的法则

常数的微分

其中，\(c\) 为常数。

线性法则

相加再微分等于微分再相加，常数提外面

其中， 一元函数 \(u=u(x),v=v(x)\) 或多元函数 \(u=u(x,y),v=v(x,y)\) ， \(c_1,c_2\) 为常数。

乘积法则

前微后不微 + 前不微后微

其中， 一元函数 \(u=u(x),v=v(x)\) 或多元函数 \(u=u(x,y),v=v(x,y)\) 。

商法则

(上微下不微 减 上不微下微）除以（下的平方）

其中， 一元函数 \(v=v(x) \neq0,u=u(x)\) 或多元函数 \(v=v(x,y) \neq 0, u=u(x,y)\) 。

矩阵变元函数的微分

向量可以看做一种特殊的矩阵

向量变元的实值标量函数

它其实就是多元函数，设其可微，则它的全微分（结果是标量，所以可以写成迹的形式）

矩阵变元的实值标量函数

它也是多元函数，设其可微，则它的全微分：

我们从这个结果中发现，它其实就是矩阵 \((\frac{\partial f}{\partial x_{ij}})_{i=1,j=1}^{m,n}\) 与矩阵 \((\mathbb{d}x_{ij})_{i=1,j=1}^{m,n}\) 对应位置的元素相乘并相加，因为结果是标量，所以也可以写成迹的形式，即：

矩阵变元的实矩阵函数

矩阵变元的实矩阵函数，它的每个元素其实就是一个矩阵变元的实值标量函数 \(f_{ij}(\pmb{X})\)。我们定义：设 \(f_{ij}(\pmb{X})\) 可微，则矩阵变元的实矩阵函数的矩阵微分，就是对每个位置的元素 \(f_{ij}(\pmb{X})\) 求全微分，排列布局不变，即：

四个法则

很重要，建议熟记

a.常数矩阵的矩阵微分

b. 线性法则

相加再微分等于微分再相加，常数提外面

其中，\(c_1,c_2\) 为常数。

c. 乘积法则

前微后不微 + 前不微后微

其中， \(\pmb{F}_{p \times q}(\pmb{X}),\pmb{G}_{q \times s}(\pmb{X})\)， 可以扩展到更多个矩阵相乘：

注意：此时的微分是矩阵，不能交换乘积的左右顺序。

d. 转置法则

转置的矩阵微分等于矩阵微分的转置

矩阵求导

为什么要使用矩阵微分求导

\(\pmb{X}_{m \times n}\) 自己就是矩阵变元为 \(\pmb{X}_{m \times n}\) 的实矩阵函数，它的每个元素是 \(x_{ij}\)，每个元素的全微分是 \(\mathbb d{x_{ij}}\)。

因此， \(\pmb{X}_{m \times n}\) 的矩阵微分是：

向量 \(\pmb{x}=[x_1,x_2,\cdots,x_n]^T\) 的矩阵微分是：

于是，我们刚刚讲到的矩阵微分四个法则，对于 \(\mathbb{d}\pmb{X}_{m \times n},\mathbb{d}\pmb{x}\) 也是适用的。

我们现在回到矩阵变元的实值标量函数的全微分：

可以发现在 \(\mathbb{tr}\) 中，右边的矩阵就是 \(\mathbb{d}\pmb{X}_{m \times n}\)，而左边的矩阵，其实就是矩阵变元的实值标量函数的 Jacobian 形式的导数：

因此我们可以把矩阵变元的实值标量函数的全微分写成：

这里要注意到，矩阵求导的目标其实就是去求 \(\frac{\partial f(\pmb{X})}{\partial \pmb{X}^T}\) 。所以，只要我们可以把一个矩阵变元的实值标量函数的全微分写成上面的形式，我们就找到了矩阵求导的结果。

对于向量变元的实值标量函数的全微分，同样可以写成：

因为向量可以看作是矩阵的一种特殊形式（列数为 1 的矩阵），所以我们可以把向量变元的情况一并包括在矩阵变元的情况里面就可以。

基本公式

夹层饼

其中， \(\pmb{A}\_{p \times m},\pmb{B}\_{n \times q}\) 是常数矩阵。这里可以进一步扩展到任意矩阵变元的矩阵函数

行列式

其中，\(\pmb{X}_{n \times n}\) 。这里可以进一步扩展到任意矩阵变元的矩阵函数

逆矩阵

其中，\(\pmb{X}_{n \times n}\) 。这里可以进一步扩展到任意矩阵变元的矩阵函数

迹变换
对于实值标量函数 \(f(\pmb{X})\) ，它的全微分也是一个标量，所以有：
\(\mathbb{tr}(f(\pmb{X})) =f(\pmb{X}) ， \mathbb{tr}(\mathbb{d}f(\pmb{X}))=\mathbb{d}f(\pmb{X})\)

两式联立进而可以得到常用实值标量函数 \(f(\pmb{X})\) 的迹变换公式：
\(\mathbb{d}f(\pmb{X}) = \mathbb{d}(\mathbb{tr}f(\pmb{X}))=\mathbb{tr}(\mathbb{d}f(\pmb{X}))\)

即在 \(\mathbb{d}f(\pmb{X})\) 的微分符号 \(\mathbb{d}\) 的前后可以直接插入迹运算 \(\mathbb{tr}\) 而保持结果不变。

如果实值标量函数本身就是某个矩阵函数 \(\pmb{F}_{p \times p}(\pmb{X})\) 的迹，如 \(\mathbb{tr}{\pmb{F}(\pmb{X})}\) ，则由全微分的线性法则，得：

换句话说，实值矩阵函数 \(\pmb{F}_{p \times p}(\pmb{X})\) 的迹变换公式为：

注意和实值标量函数中对应公式的区别在于，上式是不等于 \(\pmb{d}(\pmb{F}_{p \times p}(\pmb{X}))\) 的，这也是显然的，因为它们一个是标量，一个是矩阵。

矩阵求导示例

第一步：迹变换

第二步：写成全微分标准形式

第三步：得出结果

第一步：迹变换

第二步：写成全微分标准形式

第三步：得出结果

其中， \(\pmb{X}_{n \times n}\) 。

第一步：迹变换

第二步：写成全微分标准形式

我们发现，这是一个复合函数的全微分， \(|\pmb{X}|\) 是多元函数， \(\log u\) 是一元函数，令 \(z=\log u,u=|\pmb{X}|\) ，则

第三步：得出结果

其中， \(\pmb{A}_{n \times n}\) 为常数矩阵， \(\pmb{X}_{n \times n},(\pmb{X}+\pmb{A})^{-2}=(\pmb{X}+\pmb{A})^{-1}(\pmb{X}+\pmb{A})^{-1}\) 。

第一步：迹变换

第二步：写成全微分标准形式

第三步：得出结果

第一步：迹变换

我们知道，对于 n 阶矩阵 \(\pmb{A},\pmb{B}\) ,有 \(|\pmb{A}\pmb{B}|=|\pmb{A}| |\pmb{B}|\)

因此，有 \(|\pmb{X}^3|= |\pmb{X}\pmb{X}\pmb{X}| = |\pmb{X}||\pmb{X}||\pmb{X}| = |\pmb{X}|^3\)

所以 \(\begin{align} \mathbb{d}|\pmb{X}^3| =\mathbb{d}(|\pmb{X}|^3)= \mathbb{tr}(\mathbb{d}(|\pmb{X}|^3)) \end{align}\)

第二步：写成全微分标准形式

我们发现，这是一个复合函数的全微分， \(|\pmb{X}|\) 是多元函数， \(u^3\) 是一元函数，令 \(z=u^3,u=|\pmb{X}|\) ，则

第三步：得出结果

本栏目推荐文章
• 矩阵乘法代码
• 螺旋矩阵 59
• 数学基础(一)-标量、向量、矩阵、张量以及各范数的含义
• 矩阵相关知识图谱
• 实现自定义算子：逆矩阵inverse
• 跟踪微分器TD
• 机器学习-矩阵
• 顺时针旋转矩阵
• OpenCV实现反解法数字微分纠正，生产单张航空影像的正射影像
• OpenCL使用local内存优化矩阵乘法例子

矩阵 微分角速度 微分 矩阵 方程 数值 解法 微分 矩阵 数学基础 微分 矩阵 数学 矩阵 微分 微分 微分学 微分167 微分2.5 微分 机器 导数 微分