NOIP2023模拟9联测30 总结

题目

T1 上海

大意

判断是否存在 \(n\) 正整数，使得 \(n^2\) 是 \(k\) 的倍数，且 \(n\) 不是 \(k\) 的倍数。如果存在，输出最小的 \(n\) ；不存在输出 \(-1\) 。

\(k\leq 10^{12}\)

赛时思路

对于 \(n\) 来说，\(n\) 一定要包含 \(k\) 有的质因数，而且 \(n\) 不可包含其它质因数。 \(n\) 要最小，理想状态下 \(n^2\) 的各个质因子次数最好刚刚等于 \(k\) 的质因子次数。不难发现 \(n\) 的质因子取 \(\lceil \frac{p_i}{2} \rceil\) 最好。\(p_i\) 表示 \(k\) 的第 \(i\) 个质因子的 \(p_i\) 次方。

正解思路

同赛时思路。

T2 华二

大意

给你一个数列 \(n\)，若 \(\gcd(a_i,a_{i+1})\ne 1\) 可以交换 \(a_i\) 和 \(a_{i+1}\)。

\(1 \leq a_i \leq 9,n \leq 10^5\)

赛时思路

分析出 \(6\) 可以分为若干段，其他的可以将 \(2,4,8\) 分为一组，\(3,9\) 分为一组，\(1,5,7\) 分为一组。要求 \(2,4,8\) 和 \(3,9\) 内部有序，\(1,5,7\) 可以任意跨越。然后就不会了，甚至连组合选位置放置 \(2,4,8\) 是可以保证有序的都没想到……

正解思路

分组后可以用组合统计 \(2,4,8\) 和 \(3,9\) 放置的有序方案，然后在全局统计 \(1,5,7\) 的方案，最后乘起来统计方案数即可。

T3 高爸

大意

有 \(n\) 个数，有两个操作，可以耗费 \(a\) 选择一个数加 \(1\) 或者耗费 \(b\) 选一个数减 \(1\)，对于每个 \(i\)，求使 \(a_1,\cdots,a_i\) 相同的最小花费。

\(n \leq 10^5\)

赛时思路

列出了如下及时答案的算式：

\[a(n \times x-\sum_{i=1}^{n+m} p_i (p_i>x))+b(\sum_{i=1}^{n+m} p_i (p_i \leq x) - m \times x) \]

发现有三分性质，但不是很会三分，想其他方法又没想到，被迫开始码。

结果写完过去了 \(1h30min\)……

正解思路

博客链接：NOIP2023模拟9联测30 T3 高爸 - 彬彬冰激凌 - 博客园 (cnblogs.com)

设现在的平均力量值为 \(x\)，大于 \(x\) 力量值的龙有 \(n\) 条，小于等于的龙有 \(m\) 条，花费为：

\[a(n \times x-\sum_{i=1}^{n+m} p_i (p_i>x))+b(\sum_{i=1}^{n+m} p_i (p_i \leq x) - m \times x) \]

对于 \(a(n \times x-\sum_{i=1}^{n+m} p_i (p_i>x))\) 和 \(b(\sum_{i=1}^{n+m} p_i (p_i \leq x) - m \times x)\) 来说，都具有三分性质，凹函数的和也具有三分性质，所以可以三分。

这里写的是关于 \(x\) 值域的三分。

将 \(p_i\) 离散化后，钦定 \(x\) 后求答案时，使用树状数组求 \(p_i\) 的前缀和和小于 \(x\) 的个数。

三分时间复杂度 \(\log n\)，树状数组时间复杂度 \(\log n\)，总复杂度 \(O(n \log^2 n)\)。

T4 金牌

大意

有一棵 \(n\) 点的树，边长为 1，一条路径的长度为 \(d\)，那么代价为 \(2^d\)。

有 \(q\) 个询问，每次询问两个点 \((x,y)\) 求经过 \((x,y)\) 的路径代价的和。

\(n,q \leq 10^6\)

赛时思路

赛时想到可以分段统计代价，接着发现了错误的结论，导致分段统计被彻底抛弃……

然而正解需要分段统计。

而且暴力也需要分段统计……

正解思路

博客链接：NOIP2023模拟9联测30 T4 金牌 - 彬彬冰激凌 - 博客园 (cnblogs.com)

思路非常简单，可考试就是想歪成统计指数了……

将一条穿过 \((x,y)\) 的路径 \((u,v)\) 分为 \(u \to x \to y \to v\)，所以说对答案的贡献为：

\[2^{dis(u,x)+dis(x,y)+dis(y,v)}=2^{dis(u,x)}\times 2^{dis(x,y)}\times 2^{dis(y,v)} \]

如果把 \((x,y)\) 的路径上的边断开，形成了若干联通块，设 \(x\) 所在的联通块为 \(E_x\)，\(y\) 所在的联通块为 \(E_y\)，答案为：

\[2^{dis(x,y)} {\sum_{i\in E_x} 2^{dis(i,x)}} \sum_{i=E_y} 2^{dis(y,i)} \]

有了这个式子可以可以分类讨论求答案。

先以 1 为根建树。

若 u,v 的 lca 不是 u,v 中一点

可以通过 \(sum_u=2\times\sum\limits_{v\in u.sons} sum_v\)，预处理出子树 \(u\) 内到 \(u\) 的价值，\(y\) 同理。

又可以通过 \(dep_u+dep_v-2\times dep_{lca(u,v)}\) 求出 \(u\) 和 \(v\) 两点间的距离。（\(dep\) 是以 1 为根时的深度）

代入公式即可求值。

若 u,v 的 lca 是 u,v 中一点

这样就比较复杂了，画一张图：

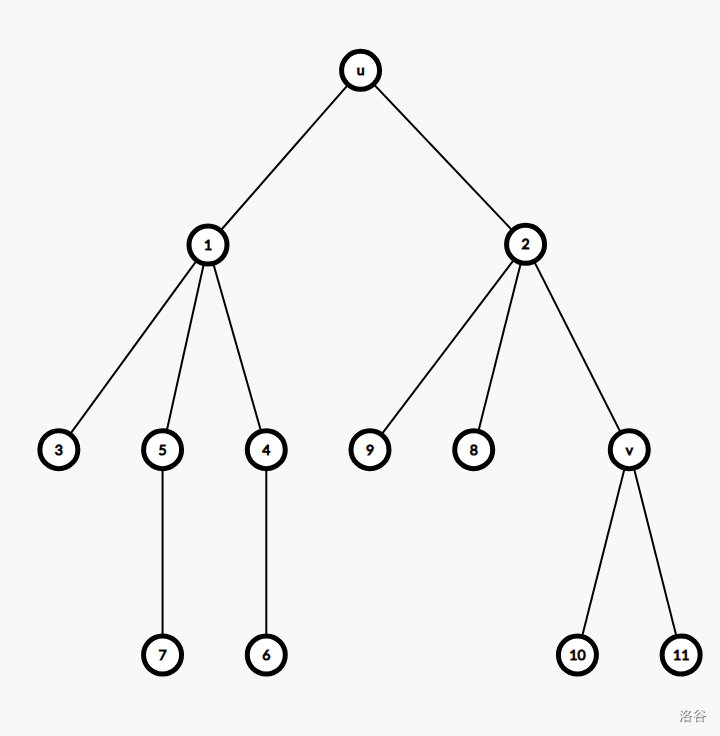
发现当 \(u\) 为根时，答案就是 \(v\) 子树内的距离和乘上距离的贡献再乘树\(u\)的距离和减去 \((u,v)\) 路径上 \(u\) 的儿子子树内的距离和。

格式化就是 \((sum_u-sum_{u.son})\times 2^{dis(u,v)}\times sum_v\)。

\(u\) 做为根时 \(u\) 的 \(sum\) 可以换根 dp 快速求，\(sum_v\) 和 \(sum_{u.son}\) 可以直接用以 1 为根时求的 \(sum\)，距离可以用上述讨论的式子求。

\(u.son\) 可以倍增时较深的节点先跳到较浅节点深度 \(-1\) 的位置，查看如果此时较深节点的父亲是较浅的节点，就可以判断为这种情况，并且使 \(u.son\) 等于当前较深节点。

CODE

文中使用倍增求 lca。

#include<bits/stdc++.h>
using namespace std;

#define ll long long

#define mod 998244353

#define S second

#define F first


const int maxn=2e6+5;

struct node
{
    int to,nxt;
}edge[maxn*2];

int n,tot;
int head[maxn],f[maxn][25],deep[maxn];

ll ans[maxn],sum[maxn];

vector< pair<int,int> >E[maxn];

ll ksm(ll x,ll y)
{
    ll sum=1;
    for(;y;y/=2,x=x*x%mod) if(y&1) sum=sum*x%mod;
    return sum;
}

void add(int x,int y)
{
    tot++;
    edge[tot].to=y;
    edge[tot].nxt=head[x];
    head[x]=tot;
}

void dfs(int u)
{
    sum[u]=1;
    for(int i=head[u];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(v==f[u][0]) continue;
        deep[v]=deep[u]+1;
        f[v][0]=u;
        for(int j=1;j<=20;j++) f[v][j]=f[f[v][j-1]][j-1];
        dfs(v);
        sum[u]=(sum[u]+sum[v]*2%mod)%mod;
    }
}
pair<int,int> Lca(int x,int y)
{
    if(deep[x]<deep[y]) swap(x,y);
    for(int i=20;i>=0;i--) if(deep[f[x][i]]>deep[y]) x=f[x][i];
    if(f[x][0]==y) return make_pair(f[x][0],x);//情况 2，返回 lca 和 u.son
    if(deep[x]>deep[y]) x=f[x][0];
    for(int i=20;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
    return make_pair(f[x][0],0);
}

void dfs_hg(int u,ll dis)//换根 dp
{
    if(u!=1) dis=((dis-sum[u]*2%mod+mod)%mod*2%mod+sum[u])%mod;
    for(pair<int,int> v:E[u]) ans[v.S]=(ans[v.S]*((dis-sum[v.F]*2+mod)%mod))%mod;
    for(int i=head[u];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(v==f[u][0]) continue;
        dfs_hg(v,dis);
    }
}

int main()
{
    scanf("%d",&n);
    for(int i=1;i<n;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);
        add(y,x);
    }

    deep[1]=1;
    dfs(1);

    int m;
    scanf("%d",&m);
    for(int i=1;i<=m;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        pair<int,int> lca=Lca(x,y);//first 是 lca，seoncd 是 u.son
        if(lca.S)
        {
            E[lca.F].push_back(make_pair(lca.S,i));
            int k=x;
            if(lca.F==x) k=y;
            ans[i]=sum[k]*ksm(2,deep[x]+deep[y]-2*deep[lca.F])%mod;
        }
        else ans[i]=sum[x]*ksm(2,deep[x]+deep[y]-2*deep[lca.F])%mod*sum[y]%mod;
    }

    dfs_hg(1,sum[1]);

    for(int i=1;i<=m;i++) printf("%lld\n",(ans[i]+mod)%mod);
}

结束了吗？

尽管倍增和树剖的时间复杂度来到了优秀的 \(O(\log n)\) 但这题卡常，我们不得不用 \(O(1)\) 的预处理 lca。

啊这.jpg

lca 部分见博客预处理 O(1) 求 lca。（后面填）

在求 lca 的过程中，我们可以使用手写栈存下这一个节点的所有祖先，后面遍历虚边时，如果连接的点在栈中，那么 u.son 就等于栈中连接的点的下一个位置。

CODE

#include<bits/stdc++.h>
using namespace std;

#define ll long long
#define mod 998244353
#define S second
#define F first
#define ri register int

const int maxn=1e6+5;

struct node
{
    int to,nxt;
}edge[maxn*2];

int n,tot,tp;
int head[maxn],deep[maxn],x[maxn],y[maxn],vis[maxn],stk[maxn],fa[maxn];

ll ans[maxn],sum[maxn];

pair<int,int> Lca[maxn];

vector< pair<int,int> >E[maxn],EL[maxn];

inline int read() {
    int s = 0, w = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        if (ch == '-')
            w = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') s = s * 10 + ch - '0', ch = getchar();
    return s * w;
}
inline void write(ll X)
{
    if(X<0) {X=~(X-1); putchar('-');}
    if(X>9) write(X/10);
    putchar(X%10+'0');
}

inline ll ksm(ll x,ll y)
{
    ll sum=1;
    for(;y;y/=2,x=x*x%mod) if(y&1) sum=sum*x%mod;
    return sum;
}

inline void add(int x,int y)
{
    tot++;
    edge[tot].to=y;
    edge[tot].nxt=head[x];
    head[x]=tot;
}

inline int frt(int u)
{
    if(fa[u]==u) return u;
    return fa[u]=frt(fa[u]);
}
inline void dfs(int u)//O(1) lca
{
    stk[++tp]=u;
    vis[u]=tp;//u 节点在栈中的位置
    sum[u]=1;
    for(ri i=head[u];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(vis[v]) continue;
        deep[v]=deep[u]+1;
        dfs(v);
        fa[v]=u;
        sum[u]=(sum[u]+sum[v]*2%mod)%mod;
    }
    for(pair<int,int> i:EL[u])
    {
        if(vis[i.F]!=-1&&vis[i.F]!=0) Lca[i.S].S=stk[vis[i.F]+1];//如果栈，但没出栈，u.son 赋值
        else if(vis[i.F]) Lca[i.S].F=frt(i.F);
    }
    tp--;
    vis[u]=-1;//-1 表示入过栈，但已出栈
}

inline void dfs_hg(int u,ll dis,int f)
{
    if(u!=1) dis=((dis-sum[u]*2%mod+mod)%mod*2%mod+sum[u])%mod;
    for(pair<int,int> v:E[u]) ans[v.S]=(ans[v.S]*((dis-sum[v.F]*2+mod)%mod))%mod;
    for(ri i=head[u];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(v==f) continue;
        dfs_hg(v,dis,u);
    }
}

int main()
{
    n=read();
    for(ri i=1;i<n;i++)
    {
        int x,y;
        x=read(),y=read();
        add(x,y);
        add(y,x);
    }

    int m;
    m=read();
    for(ri i=1;i<=m;i++) 
    {
        x[i]=read(),y[i]=read();
     	EL[x[i]].push_back(make_pair(y[i],i)),EL[y[i]].push_back(make_pair(x[i],i));//虚边
    }

    for(ri i=1;i<=n;i++) fa[i]=i;
    dfs(1);

    for(ri i=1;i<=m;i++)
    {
        pair<int,int> lca=Lca[i];
        if(lca.S)
        {
            E[lca.F].push_back(make_pair(lca.S,i));
            int k=x[i];
            if(lca.F==x[i]) k=y[i];
            ans[i]=sum[k]*ksm(2,deep[x[i]]+deep[y[i]]-2*deep[lca.F])%mod;
        }
        else ans[i]=sum[x[i]]*ksm(2,deep[x[i]]+deep[y[i]]-2*deep[lca.F])%mod*sum[y[i]]%mod;
    }

    dfs_hg(1,sum[1],0);

    for(ri i=1;i<=m;i++) write((ans[i]+mod)%mod),putchar('\n');
}

有一个小技巧需要tarjin预处理 \(O(1)\) 求 LCA。