1. 线性可分支持向量机

线性可分支持向量机（Linearly Separable Support Vector Machine）是支持向量机中的一种特例，用于解决线性可分的分类问题。它的目标是找到一个超平面，将不同类别的数据点分隔开，同时最大化分类的间隔。

首先，我们来定义线性可分的SVM的目标函数，通常称为硬间隔支持向量机问题。给定一个训练数据集 ${(x_i, y_i)}$，其中 $x_i$ 是输入特征向量，$y_i$ 是类别标签（$y_i \in \{-1, 1\}$）。我们的目标是找到一个超平面的法向量 $w$ 和截距 $b$，使得以下不等式对于所有训练样本成立：$y_i(w \cdot x_i - b) \geq 1$

线性可分支持向量机的最优化问题公式如下：

\[\begin{align*} & \text{max} \quad \frac{1}{2}\|w\|^2 \\ & \text{s.t.} \quad y_i(w \cdot x_i - b) \geq 1, \quad \ i = 1, 2, \ldots, m \end{align*} \]

这里，$w \cdot x_i$ 表示内积操作，$w \cdot x_i = \sum_{j=1}^{n} w_j x_{ij}$，其中 $n$ 是特征向量的维度。不等式 $y_i(w \cdot x_i - b) \geq 1$ 表示所有样本点都远离超平面，并且分类没有错误。

为了形式化这一目标，我们可以定义一个拉格朗日乘子 $\alpha_i$ 来表示每个不等式约束。然后，我们可以构建拉格朗日函数 $L(w, b, \alpha)$，如下所示：

\[L(w, b, \alpha) = \frac{1}{2}\|w\|^2 - \sum_{i=1}^{m} \alpha_i[y_i(w \cdot x_i - b) - 1] \]

接下来，我们可以通过最大化拉格朗日函数 $L(w, b, \alpha)$ 来解决问题。为了最大化 $L(w, b, \alpha)$，需要满足以下条件：

求解 $\max_{\alpha} L(w, b, \alpha)$。
通过等式约束 $\sum_{i=1}^{m} \alpha_i y_i = 0$ 来满足 $\alpha_i$ 的限制。
最终，通过最大化 $L(w, b, \alpha)$ 得到 $\alpha^*$，然后可以使用以下公式计算法向量 $w$：

\[w^* = \sum_{i=1}^{m} \alpha_i^* y_i x_i \]

并计算截距 $b$：

\[b^* = y_j - w^* \cdot x_j \]

其中 $x_j$ 是支持向量（满足 $\alpha_j^* > 0$ 的样本）。这样，我们就可以获得分隔超平面的法向量 $w$ 和截距 $b$，从而完成了线性可分支持向量机的训练。

2. 软间隔最大化

异常点会导致数据线性不可分，即意味着某些样本点不能满足函数间隔大于等于1的约束条件，为了解决该问题可以对每个样本点${(x_i, y_i)}$引进一个松弛变量$\xi _i > 0$，使得函数间隔加上松弛变量大于等于1，因此约束条件将变成$$y_i(w \cdot x_i - b) \geq 1-\xi _i $$

相比较硬间隔最大化，可以看到样本到分离超平面的函数距离要求放松了，之前一定要大于等于1，现在只需要加上一个大于等于0的松弛变量大于等于1即可。同时，每个松弛变量$\xi _i > 0$对应一个代价$\xi _i > 0$，则目标函数变成了

\[\quad \frac{1}{2}\|w\|^2 + C\sum_{i=1}^{m}\xi_i \]

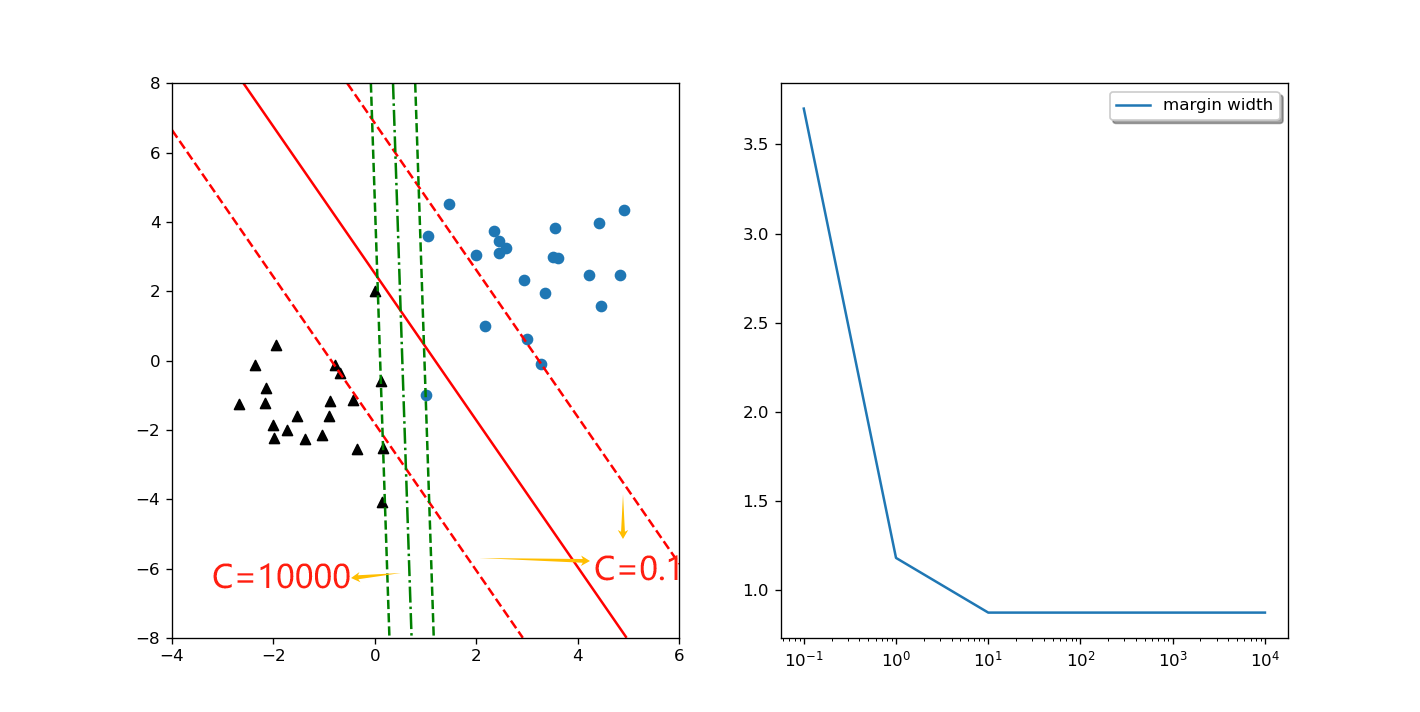
其中$C>0$称为惩罚参数，C值越大，对误分类样本惩罚越大，即间隔宽度越小，C值越小，对误分类样本惩罚越小，即间隔宽度越大。

(代码参考https://github.com/GenTang/intro_ds/blob/master/ch08-supervised/svm/hard_soft_margin.py）现在的目标函数有两层意思，即希望$\frac{1}{2}\|w\|^2$尽量小的同时误分类样本也尽可能的少，C则是协调两者关系的正则化惩罚系数。上面的思路较于硬间隔最大化称为软间隔最大化，也因此线性支持向量机的原始问题为 $$ \text{min} \quad \frac{1}{2}\|w\|^2 + C\sum_{i=1}^{m}\xi_i \\ \begin{align*} & y_i(w \cdot x_i - b) \geq 1 - \xi_i, i = 1, 2, \ldots, m \\ & \xi_i \geq 0, i = 1, 2, \ldots, m \end{align*} $$

3. 核函数

核函数找到一个非线性的空间变换$\phi$,将数据转换为$\{\phi(X_i),y_i\}$,再找两者的关系，与神经网络里的隐藏层类似

526互联

6.支持向量机

1. 线性可分支持向量机

2. 软间隔最大化

3. 核函数