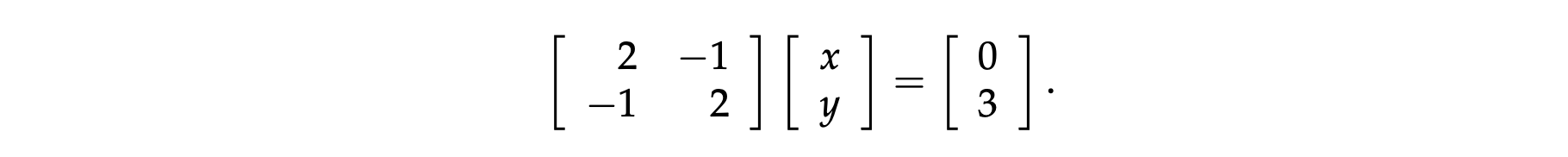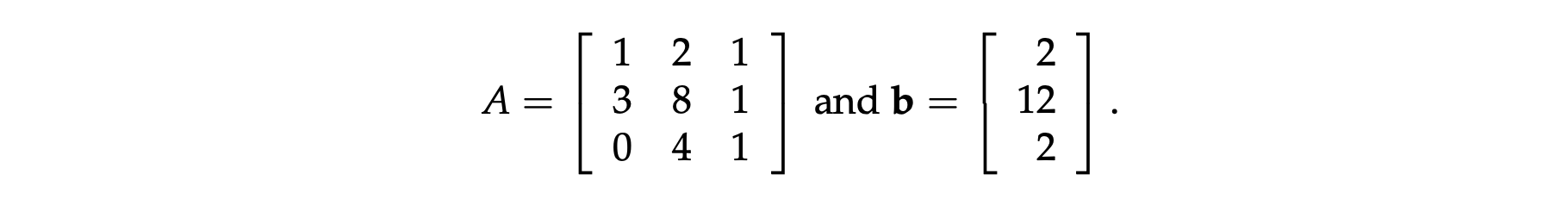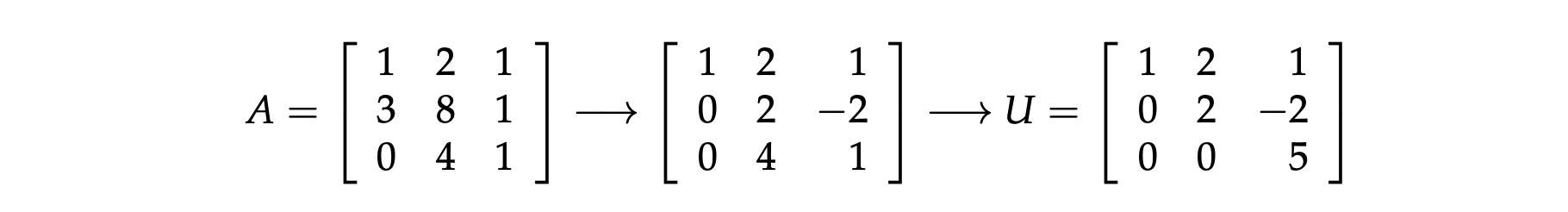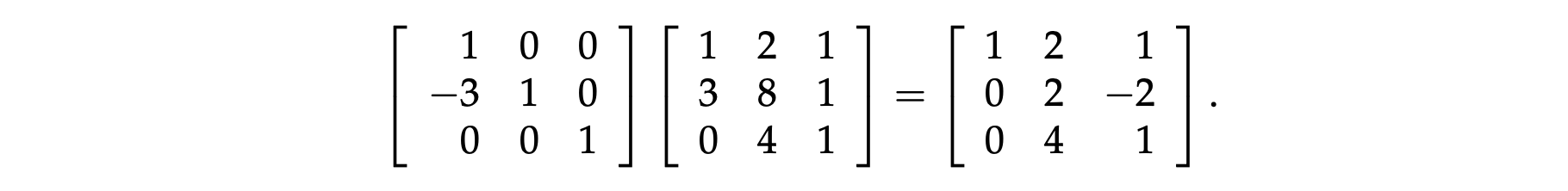MIT 18.06 线性代数 学习笔记
Lecture 1
线性方程组的几何化
e.g.
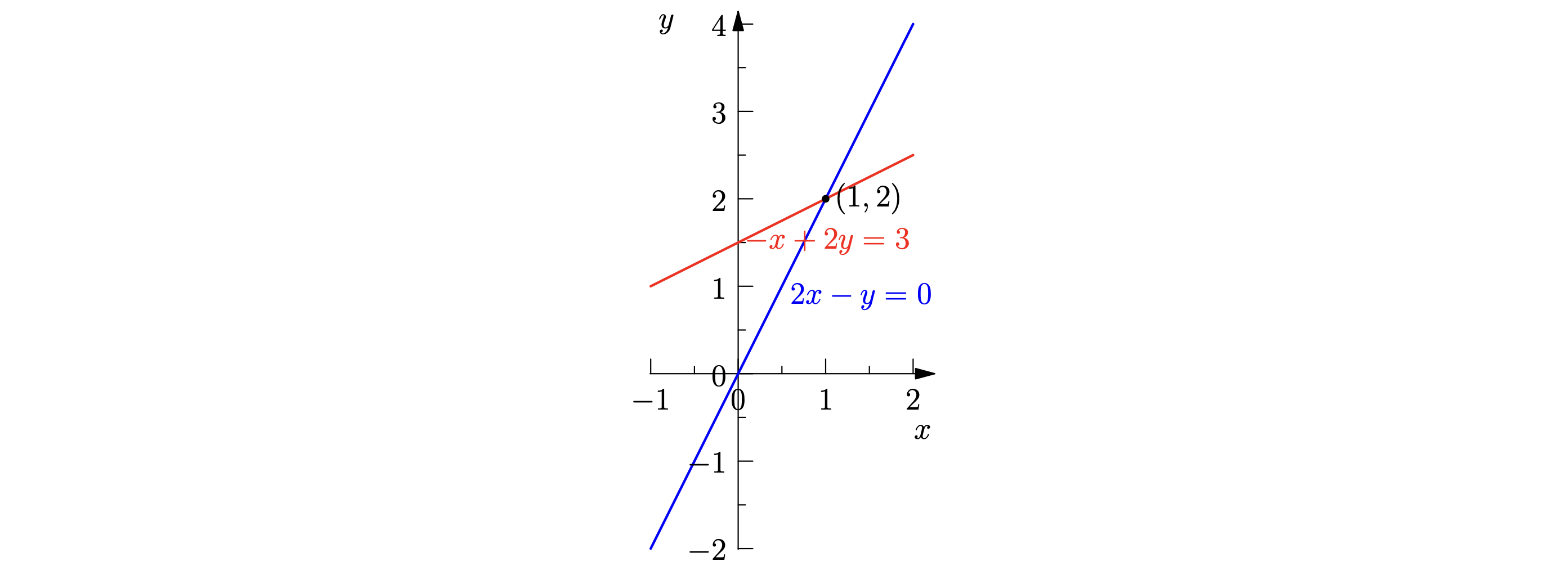
行视角(Row Picture):解集是直线们的交点 或 平面们的交线等。
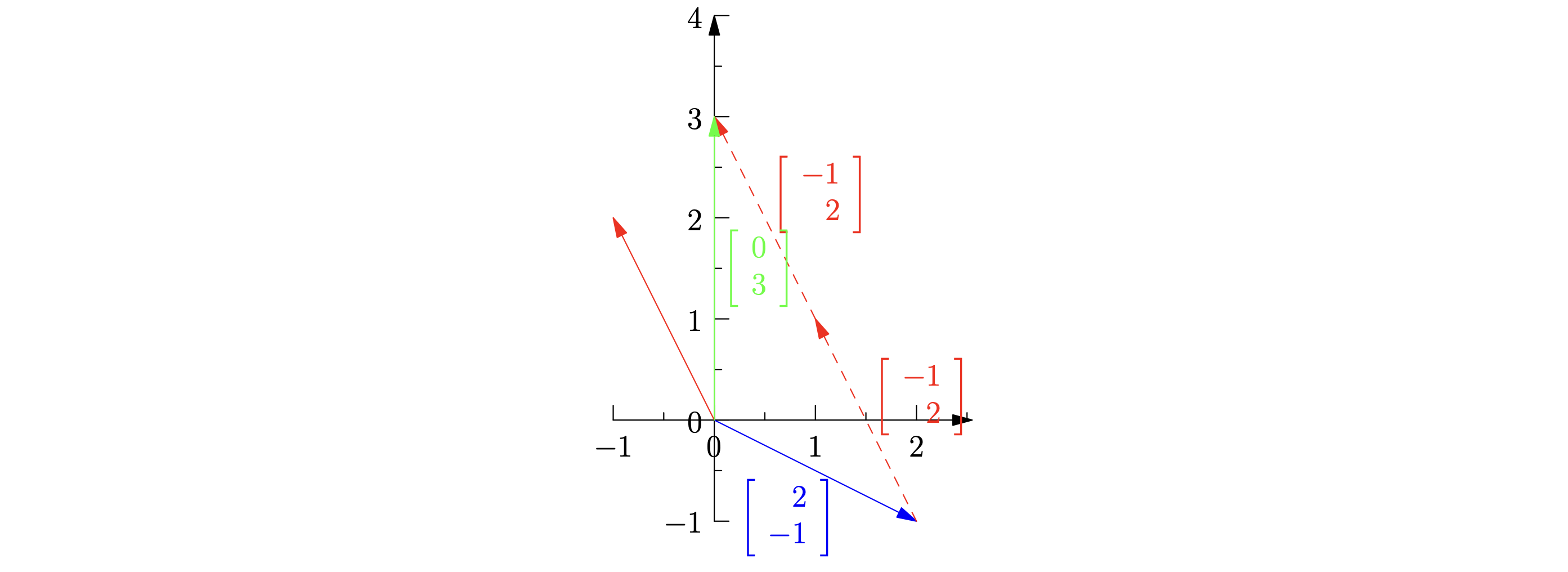
列视角(Column Picture):找到已知向量组的线性组合,来表达出目的向量。
矩阵视角(Matrix Picture):写成 A\(x\) = \(b\) 的形式,其中 A 是系数矩阵,x 是未知数向量,b 是结果向量。
线性不相关 (Linear Independence)
给定矩阵 A ,若对于任意一个向量 b ,都能找到一个向量 x 满足 A\(x\) = \(b\),则说明向量 x 的线性组合"可以触碰到所处空间的任何一个角落"(二维平面、三维空间......)。
若不能,则称 A 矩阵为奇异矩阵(singular matrix),在这个奇异矩阵中的列向量们是线性相关的(linearly dependent),因此向量 x 所有的线性组合总是汇集在一个点/一条线/一个平面/...上,向量 x 的线性组合不能触碰到所处空间的任何一个角落。
Lecture 2
消元 (Guass Elimination)
求解线性方程组的解时,若采用矩阵视角,可以写成 A\(x\) = \(b\)。
e.g.
然后通过消元求解出未知数向量 \(x\) 即可 ( A 保证可逆时),步骤如下:
1. 找到该行的 pivot ,将下面每行该位置的数变成 0 (We recopy the first row, then multiply the numbers in it by an appropriate value and subtract those values from the numbers in the second row.)
2. 若该行的 pivot 为 0 ,可以通过把后续行与该行进行交换,来继续消元
3. 直到 A 变成一个上三角矩阵 U(upper triangular matrix),停止消元。
通过消元,我们把 A\(x\) = \(b\) 变成了 U\(x\) = \(c\) ,接着通过回代法(back substitution)便可以得到原方程的解。
消元中 A 在变成 U 的过程,可以通过矩阵乘法来描述。每次的 1 过程,都可以表示成在当前矩阵的左侧乘上了一个消元矩阵(下图左侧的消元矩阵叫做 \(E_{21}\),因为我们正在想办法将矩阵中第 2 行第 1 列的数字消去。)
所以上述例子的 A 到 U 可以描述为 \(E_{32}(E_{31}(E_{21}A)) = U\),也可以写成:
有趣的性质也可以被发现:
若想对 A 进行行变换,则在 A 左边乘上对应的行变换矩阵。
若想对 A 进行列变换,则在 A 右边乘上对应的列变换矩阵。
e.g.
Lecture 3
Matrix Multiplication
Assume matrix \(C\) is the result of matrix \(A\) times matrix \(B\) , in other words \(C = AB\).
There are four ways to understand the multiplication.
1. Row times column
\(c_{ij}\) equals the dot product of row \(i\) of matrix \(A\) and column \(j\) of matrix \(B\). In other words, \(c_{ij} = \sum_{k = 1} ^ {n} a_{ik} \cdot b_{kj}\).
2. Rows
The rows of \(C\) are combinations of rows of \(B\).
3. Columns
The columns of \(C\) are combinations of columns of \(A\).
4. Column times row
The product of an \(m \times 1\) vector with a \(1 \times p\) vector is a \(m \times p\) matrix.
The columns of this matrix are multiples of the column of \(A\).
The rows of this matrix are multiples of the row of \(B\).
Blocks
\(A_i\) , \(B_j\) and \(C_k\) are matrixs, \(A_i\) are blocks of a bigger matrix and \(B_j\) are blocks with the same cutting methods like \(A_i\). What amazing is that it still fits the rules of matrix multiplication.
In other words, \(C_1 = A_1B_1 + A_2B_3.\)
Inverses
How to understand inverse matrix
For understand the inverse matrix easily, we need to use the Elimination Matrix which we have metioned in the lecture 2.
Assume a elimination matrix \(E_{21} = \left[\begin{array}{c} 1 & 0 & 0 \\ -3 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]\), the second row of \(E_{21}\) means subtracting \(3\) times row \(1\) from row \(2\).
To “undo” this operation we must add \(3\) times row \(1\) to row \(2\) using the inverse matrix:
It is obviously that \(E_{21}^{-1}E_{21} = E_{21}E_{21}^{-1} = \left[\begin{array}{c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] = I\).
Defination of inverse martix
If \(A\) is a square matrix, the most important question you can ask about it is whether it has an inverse \(A^{−1}\). If it does, then \(A^{−1}A = I = AA^{−1}\) and we say that \(A\) is invertible or nonsingular.
For a singular matrix \(A\) , which means \(A\) doesn't have its corresponding inverse matrix \(A^{-1}\), it can be proved that we can always find some non-zero vector \(x\) which \(Ax = 0\).
This conclusion can be proved by using reduction to absurdity. Assume \(A\) has its inverse matrix \(A^{-1}\), then \(Ax = 0\) is equivalent to \(A^{-1}Ax = A^{-1} \cdot 0\), which means \(x = 0\). But the precondition is that \(x\) is an non-zero vector. Thus contradiction occurs so that singular matrices don't have their inverse matrices.
Gauss-Jordan Elimination
We combine the method of Guass Elimination with block matrices to get the Gauss-Jordan Elimination. The main idea is:
\(E\) is the product of all of the elimination matrices during the process of transforming \(A\) to \(I\) using Guass Elimination.
The correctness of this method is obviously due to \(EA = I\). According to the defination of inverse martix, \(E = A^{-1}\).