Ignore Operations

题意

Takahashi 有一个整数 \(x\)，初始 \(x = 0\)。

有 \(n\) 次操作。第 \(i\) 次操作用两个整数 \(t_i, y_i\) 描述：

如果 \(t_i = 1\)，将整数 \(x\) 替换为 \(y_i\)。
如果 \(t_i = 2\)，将整数 \(x\) 替换为 \(x + y_i\)。

Takahashi 可以跳过其中至多 \(K\) 次操作。对于剩下的没跳过的操作序列，按顺序执行操作，并求出最终 \(x\) 的可能最大值。

数据范围

\(0 \leqslant k \leqslant n \leqslant 2 \times 10^5, n \geqslant 1\)
\(t_i \in \{ 1, 2\}, |y_i| \le 10^9\)

思路

我们肯定不会跳过那些对答案有正面作用的操作，那其他的呢？

来看一张草图。

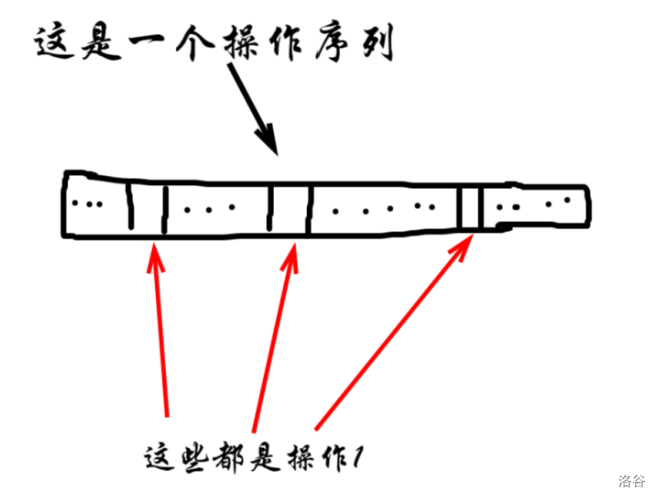
显然，在最后一次赋值操作以前，所有操作均可视为没有。

那么在最后一次赋值操作之后的那些操作呢？跳过第 \(i\) 次操作的话，对答案的贡献就是：\(-y_i\)，当我们跳过次数超过 \(k\) 时，我们要做出取舍：把对答案贡献最小的那一次放弃。

那么，我们可以推出第一步：从后往前找，用堆来存储每次操作对答案的贡献，模拟一下上面的那种操作即可。

那问题是，处理好了最后一次赋值操作以后的所有，那前面的怎么办呢？

这也不难，令 \(sum_i\) 表示从操作 \(1\) 执行到操作 \(i\)、一次也不跳过的情况下的答案，那么删除最后一次赋值操作(\(j\))对答案的贡献就是 \(sum_{i - 1} - sum_i\)，且这次操作是不可逆的，即永久消耗这次操作。

统计答案即可。

复杂度

时间：\(O(n \log n)\)
空间：\(O(n)\)

Code

点击查看代码

#include <iostream>
#include <queue>

using namespace std;
using ll = long long;

const int N = 2e5 + 10;

struct Node {
  int op, t;
} a[N];

int n, k;
ll x, y, sum[N], ans, num;
priority_queue<int> pq; // 堆维护

int main () {
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n >> k;
  for (int i = 1; i <= n; i++) {
    cin >> a[i].op >> a[i].t;
    if (a[i].op == 1) { // 预处理 sum
      sum[i] = a[i].t;
    } else {
      sum[i] = sum[i - 1] + a[i].t;
    }
    ans = sum[i];
  }
  for (int i = n; k && i >= 1; i--) {
    if (a[i].op == 2 && a[i].t < 0) { // 操作 2
      pq.push(a[i].t); // 答案贡献，这里取了个反
      num += a[i].t; // 贡献之和
      if (pq.size() > k) { // 操作次数超过 k
        num -= pq.top(), pq.pop(); // 去掉答案贡献最小的
      }
    } else if (a[i].op == 1) { // 操作 1
      num += sum[i] - sum[i - 1];
      if (pq.size() == k) {
        num -= pq.top(), pq.pop();
      }
      k--; // 不可逆的操作
    }
    ans = max(ans, sum[n] - num); // 计算答案最大值
  }
  cout << ans;
  return 0;
}