[PA 2022] Wielki Zderzacz Termionów
有 \(n\) 个球,每个球有 A、B 或 C 三种颜色。开始时你将每个 C 涂成 A 或 B。之后的每次操作,你可以选择相邻的两个 A 合并为一个 B,或选择相邻的两个 B 合并为一个 A。求将 C 涂色的方案数,满足你能够通过若干次操作使得只剩下一个球。有 \(q\) 次修改,每次改变一个球的颜色,你需要对每次修改求出答案。答案对 \(10^9 + 7\) 取模。
\(n \leq 2 \times 10^5\),\(q \leq 10^5\)。
首先当然需要找到合法的充要条件。注意到题目中的操作和 \(3\) 进制加法有着神秘的关联,即把 A 视为 \(1\),B 视为 \(2\),有 \(1+1 \equiv 2 \pmod{3}\) 和 \(2+2 \equiv 1 \pmod{3}\),我们试着从这个角度考虑。\(n=1\) 平凡,对于 \(n>1\) 的情况这里直接给出结论:合法当且仅当存在至少一对相邻球的颜色相同,并且序列的总和 \(s\) 满足 \(s \bmod 3 \neq 0\)。
由于每次操作不会改变 \(s \bmod 3\) 的值,并且显然如果不满足第一个条件那么一定没救,于是必要性得证。接着考虑充分性,发现唯一可能阻止我们合并到只剩下最后一个球的情况是,在合并中出现了某个时刻,剩下的球数 \(>1\),并且相邻球的颜色均不相同。这点也很容易避免,只需要在要合并到边界上的时候往反方向合并就行了。于是充分性得证。故结论成立。
这时候我们惊喜的发现,我们居然不怎么需要管 A 和 B 在序列中具体是怎么分布的了!具体来说,设所有 C 在涂完色后的总和为 \(s'\),那么限制可以写成 \(s' \equiv k \pmod{3}\) 的形式,这可以通过 DP 预处理出来,容易 \(\mathcal{O}(1)\) 回答询问。再简单维护一下所有相邻颜色均不同的方案数即可。代码中是容斥成算不合法的方案数,此时注意当 \(2 \mid n\) 时,所有相邻颜色均不同的情况在容斥的时候已经减掉了,需要特判一下。时间复杂度 \(\mathcal{O}(n+q)\)。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 2e5 + 5, mod = 1e9 + 7;
int n, q, sum, all, c1, c2, h[N], f[N][3]; bool ok;
char s[N];
void add(int x) {
if (s[x] == 'N') all++;
else sum = (sum + (s[x] == 'C' ? 1 : 2)) % 3;
if ((x % 2 == 1 && s[x] == 'Z') || (x % 2 == 0 && s[x] == 'C')) c1++;
if ((x % 2 == 1 && s[x] == 'C') || (x % 2 == 0 && s[x] == 'Z')) c2++;
}
void del(int x) {
if (s[x] == 'N') all--;
else sum = (sum + (s[x] == 'C' ? 2 : 1)) % 3;
if ((x % 2 == 1 && s[x] == 'Z') || (x % 2 == 0 && s[x] == 'C')) c1--;
if ((x % 2 == 1 && s[x] == 'C') || (x % 2 == 0 && s[x] == 'Z')) c2--;
}
int calc() {
int ban = (3 - sum) % 3, ans = (h[all] + mod - f[all][ban]) % mod;
if (ok) {
if (!c1) ans = (ans + mod - 1) % mod;
if (!c2) ans = (ans + mod - 1) % mod;
}
return ans;
}
signed main() {
// ios :: sync_with_stdio(false);
// cin.tie(nullptr);
cin >> n >> q;
scanf("%s", s + 1);
ok = (n > 1 && n % 2 == 1);
h[0] = 1;
for (int i = 1; i <= n; i++) h[i] = 1LL * h[i - 1] * 2 % mod;
f[0][0] = 1;
for (int i = 1; i <= n; i++) {
f[i][0] = (f[i - 1][1] + f[i - 1][2]) % mod;
f[i][1] = (f[i - 1][0] + f[i - 1][2]) % mod;
f[i][2] = (f[i - 1][0] + f[i - 1][1]) % mod;
}
for (int i = 1; i <= n; i++) add(i);
cout << calc() << "\n";
for (int i = 1, x; i <= q; i++) {
cin >> x;
char c[5]; scanf("%s", c + 1);
del(x), s[x] = c[1], add(x);
cout << calc() << "\n";
}
return 0;
}
[PA 2022] Podwyżki
给定一个长为 \(n\) 的序列,划分成 \(k\) 段使得不存在从每段各选一个元素的方案,满足这些元素严格升序。构造或输出无解。
\(2 \leq k \leq n \leq 5 \times 10^5\)。
我们的目标是,使得前面某个段的最小值不小于后面某个段的最大值。我们称这样的两个段为目标对。
特判掉整个序列严格升序的情况,此时一定存在某个位置使得 \(a_i \geq a_{i+1}\)。那么对于 \(k \geq 4\) 的情况,我们找到满足 \(a_{p} \geq a_{p+1}\) 的 \(p\),最坏的情况是先分成 \([1,p-1],\color{green}{[p,p],[p+1,p+1]}\)\(,[p+2,n]\),多出来的段数随便分就行了。
剩下 \(k=2,3\) 的情况,我们一个一个讨论。对于 \(k=2\),预处理前缀 \(\min\) 和后缀 \(\max\) 即可。
\(k=3\) 的情况麻烦一些,我们枚举第一段 \([1,p]\),如果 \([1,p]\) 内的最小值不小于 \(a_{p+1}\) 或 \(a_n\),那么直接分成 \(\color{green}{[1,p],[p+1,p+1]}\)\(,[p+2,n]\) 或者 \(\color{green}{[1,p]}\)\(,[p+1,n-1],\color{green}{[n,n]}\) 就行了。否则容易说明目标对一定在某个第 \(2\) 段和第 \(3\) 段中产生。从后往前做,需要支持每次在前面添加一个数,然后查询是否存在一个位置使得前缀 \(\min\) 不小于后缀 \(\max\)。
使用 set 维护即可,每次把后缀 \(\max\) 扔到 set 里,加入一个数 \(a_i\) 时把 set 中所有大于 \(a_i\) 的值删除,set 中剩下的就是使得前缀 \(\min\) 不小于后缀 \(\max\) 的位置了。时间复杂度 \(\mathcal{O}(n \log n)\)。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 5e5 + 5;
int n, k, a[N], fmi[N], gmi[N], gmx[N]; bool vis[N];
vector <int> ans;
struct dat {
int val, id;
bool operator < (const dat &p) const {
return val == p.val ? id < p.id : val < p.val;
}
};
set <dat> s;
signed main() {
// ios :: sync_with_stdio(false);
// cin.tie(nullptr);
cin >> n >> k;
for (int i = 1; i <= n; i++) cin >> a[i];
int ok = 0;
for (int i = 1; i < n; i++) ok += a[i] >= a[i + 1];
if (!ok) return puts("NIE"), 0;
fmi[1] = a[1];
for (int i = 2; i <= n; i++) fmi[i] = min(fmi[i - 1], a[i]);
gmx[n] = gmi[n] = a[n];
for (int i = n - 1; i >= 1; i--) gmi[i] = min(gmi[i + 1], a[i]), gmx[i] = max(gmx[i + 1], a[i]);
if (k >= 4) {
for (int i = 1; i < n; i++) {
if (a[i] >= a[i + 1]) {
if (i > 1) ans.push_back(i - 1), vis[i - 1] = 1;
ans.push_back(i), vis[i] = 1;
if (i + 1 < n) ans.push_back(i + 1), vis[i + 1] = 1;
break;
}
}
if (ans.size() < 3) k += (3 - ans.size());
k -= 4;
for (int i = 1; i < n; i++) {
if (!k) break;
if (!vis[i]) ans.push_back(i), vis[i] = 1, k--;
}
} else if (k == 2) {
int ok = 0;
for (int i = 1; i < n; i++)
if (fmi[i] >= gmx[i + 1]) { ans.push_back(i), ok = 1; break; }
if (!ok) return puts("NIE"), 0;
} else if (k == 3) {
int ok = 0;
for (int i = n - 1; i >= 2; i--) {
s.insert((dat){ gmx[i + 1], i + 1 });
auto it = s.upper_bound((dat){ a[i], n + 1 });
s.erase(it, s.end());
if (!s.empty()) {
auto it = s.begin();
ans.push_back(i - 1), ans.push_back(it -> id - 1), ok = 1;
break;
}
}
if (ok) goto EXIT;
for (int i = 1; i < n - 1; i++) {
if (fmi[i] >= a[n]) {
ans.push_back(i), ans.push_back(n - 1), ok = 1;
break;
} else if (fmi[i] >= a[i + 1]) {
ans.push_back(i), ans.push_back(i + 1), ok = 1;
break;
}
}
if (!ok) return puts("NIE"), 0;
}
EXIT:
sort(ans.begin(), ans.end());
puts("TAK");
for (auto z : ans) cout << z << " ";
return 0;
}
[PA 2022] Drybling Bajtessiego
给定 \(n\) 个括号串 \(s_i\),对于所有 \(i,j \in [1,n]\) 求 \(s_i + s_j\) 有多少种本质不同的合法括号子序列。答案对 \(10^9+7\) 取模。
\(n,|s_i| \leq 600\),时限 \(\text{9.0s}\)。
先考虑一个括号序列的本质不同的合法括号子序列数怎么求。用经典的子序列自动机 DP 容易做到 \(\mathcal{O}(n^2)\),这里不再赘述。当然你可能也不太需要知道子序列自动机到底是什么东西,从 “考虑钦定一种计算方式使得不会算重” 也能够推出类似的结构。
现在的问题是我们怎么把两个序列的结果拼在一起。这时候只需要考虑跨过分界的子序列,一个显然的事实是,如果在 \(s_i\) 中选的最后一个位置是 \(p\),然后选了 \(s_{j,k}\),那么 \(s_i\) 中 \(p\) 对应的后缀里都不应该出现 \(s_{j,k}\),否则和自动机的性质矛盾。于是我们可以把左边可能和右边合并的值预处理出来。接下来要面临的问题是,如果两边都从前往后 DP,合并的时候无法合并出合法括号串。对每个串预处理出反串的 DP 结果即可。这样看起来违反了一般的自动机,但由于自动机的本质也只是 “钦定一种计算方式使得不会算重”,这里相当于是对于跨过分界的子序列右边的部分,钦定在 “满足下标最大的,且后缀存在某种子序列” 的位置统计这种子序列,因此其实是没有问题的。总时间复杂度 \(\mathcal{O}(n^3)\)。
code
#include <bits/stdc++.h>
using namespace std;
const int N = 605, mod = 1e9 + 7;
void add(int &x, int y) { x = ((x + y >= mod) ? (x + y - mod) : (x + y)); }
int n, L[N], f[N][N][2], g[N][N][2], t[N][2], dp[N][N], a[N];
string s[N];
void calc1(string s, int f[N][2], int &a) {
int n = s.size();
t[n][0] = t[n][1] = n;
for (int i = n - 1; i >= 0; i--) {
t[i][0] = s[i] == 'L' ? i : t[i + 1][0];
t[i][1] = s[i] == 'P' ? i : t[i + 1][1];
}
memset(dp, 0, sizeof dp);
dp[t[0][0]][1] = 1;
for (int i = 0; i < n; i++) {
for (int j = 0; j <= i + 1; j++) {
if (!dp[i][j]) continue;
add(dp[t[i + 1][0]][j + 1], dp[i][j]);
if (j) add(dp[t[i + 1][1]][j - 1], dp[i][j]);
}
}
bool ok[2] = {0, 0};
for (int i = n - 1; i >= 0; i--) {
for (int x = 0; x < 2; x++) {
if (ok[x]) continue;
for (int j = 0; j <= i + 1; j++) if (dp[i][j]) add(f[j][x], dp[i][j]);
}
ok[s[i] == 'P'] = 1, add(a, dp[i][0]);
}
for (int x = 0; x < 2; x++) if (!ok[x]) add(f[0][x], 1);
}
void calc2(string s, int f[N][2]) {
int n = s.size();
t[n][0] = t[n][1] = n;
for (int i = n - 1; i >= 0; i--) {
t[i][0] = s[i] == 'P' ? i : t[i + 1][0];
t[i][1] = s[i] == 'L' ? i : t[i + 1][1];
}
memset(dp, 0, sizeof dp);
dp[t[0][0]][1] = 1;
for (int i = 0; i < n; i++) {
for (int j = 0; j <= i + 1; j++) {
if (!dp[i][j]) continue;
add(dp[t[i + 1][0]][j + 1], dp[i][j]);
if (j) add(dp[t[i + 1][1]][j - 1], dp[i][j]);
add(f[j][s[i] == 'P'], dp[i][j]);
}
}
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> s[i], L[i] = s[i].size();
calc1(s[i], f[i], a[i]);
reverse(s[i].begin(), s[i].end());
calc2(s[i], g[i]);
}
for (int x = 1; x <= n; x++) {
for (int y = 1; y <= n; y++) {
int ans = a[x], lim = min(L[x], L[y]);
for (int i = 0; i <= lim; i++)
for (int j = 0; j < 2; j++)
add(ans, 1LL * f[x][i][j] * g[y][i][j] % mod);
cout << ans << " \n"[y == n];
}
}
return 0;
}
[PA 2022] Fotografia
给定一个长为 \(n\) 的排列。每次操作你可以选择若干个位置,设你依次选择了 \(k\) 个位置 \(p_1,\cdots,p_k\),那么操作后 \(a'_{p_i} \gets a_{p_{k-i+1}}\)。求使得序列升序的最小操作次数并构造方案。
\(n \leq 3 \times 10^3\)。
稍微冷静一下就能发现这个操作的本质:选择若干对 \((i,j)\),交换 \(a_i,a_j\),但在每次操作中每个位置最多只能选择一次、
我们不妨先考虑一下交换 \(a_i,a_j\) 会发生什么。从置换的角度考虑,交换 \(a_i\) 和 \(a_j\) 要么会分裂一个环,要么会合并两个环。我们想要的结果是剩下 \(n\) 个自环,感性理解一下,我们一定不会执行合并操作。于是每个环之间独立了,我们可以只考虑一个环的情况。
设环长为 \(k\)。\(k \leq 2\) 的情况平凡,而对于 \(k \geq 3\) 的情况,显然我们不可能通过一次操作全都分成自环。接下来我们断言用 \(2\) 次操作一定可以做到,这点容易构造:第一次操作把环分割成若干个长度 \(\leq 2\) 的环,然后再用一次操作全都分成自环就行了。除去排序时间复杂度 \(\mathcal{O}(n)\)。
code
#include <bits/stdc++.h>
using namespace std;
typedef vector <int> vi;
const int N = 3e3 + 5;
int n, k[N]; bool vis[N];
pair <int, int> a[N];
vector <vi> ans;
signed main() {
ios :: sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i].first, a[i].second = i;
sort(a + 1, a + n + 1);
for (int i = 1; i <= n; i++) k[a[i].second] = i;
while (1) {
vi A, B;
fill(vis + 1, vis + n + 1, 0);
for (int i = 1; i <= n; i++) {
if (vis[i]) continue;
vi cyc;
for (int j = i; !vis[j]; j = k[j]) cyc.push_back(j), vis[j] = 1;
for (int l = 0, r = (int)cyc.size() - 1; l < r; l++, r--) {
swap(k[cyc[l]], k[cyc[r]]);
A.push_back(cyc[l]), B.push_back(cyc[r]);
}
}
reverse(A.begin(), A.end());
A.insert(A.end(), B.begin(), B.end());
if (A.empty()) break;
ans.push_back(A);
}
assert(ans.size() <= 2);
cout << ans.size() << "\n";
for (auto z : ans) {
cout << z.size() << "\n";
for (auto x : z) cout << x << " ";
cout << "\n";
}
return 0;
}
[PA 2022] Miny
给定一棵树,边有边权。每个点上都有一颗地雷,第 \(i\) 个地雷爆炸半径为 \(r_i\)。如果地雷 \(i\) 爆炸,所有距离这颗地雷不超过 \(r_i\) 的地雷都会爆炸。求每颗地雷引爆后会导致多少地雷爆炸。
\(n \leq 10^5\),\(c_i \leq 10^{12}\),\(r_i \leq 10^{18}\),时限 \(\text{9.0s}\)。
考虑建出一张图,如果引爆 \(i\) 后能直接引爆 \(j\),就连边 \(i \to j\)。那么最后答案就是每个点可达的点数。
由于连边的形式是向距离某个点不超过 \(k\) 的所有点连边,我们考虑点分治,将点按照与分治中心的距离排序,那么变成向序列上距离 \(\leq k'\) 的点连边,前缀优化建图即可。
但是每个点可达点数好像不太可做,我们莽一个线段树合并并相信它能过,然后它就过了。就离谱。
建图的复杂度是 \(\mathcal{O}(n \log^2 n)\)。线段树合并不太会算(有神教教吗 ),不过官方题解似乎给出了一个 \(\mathcal{O}(n \log n)\) 的高妙做法,没细看。
),不过官方题解似乎给出了一个 \(\mathcal{O}(n \log n)\) 的高妙做法,没细看。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long i64;
typedef unsigned int u32;
constexpr int N = 1e5 + 5, M = N * 60, S = 6e7;
int n; i64 eff[N];
vector <pair <int, i64>> e[N]; vector <int> t[M], G[M];
int V, siz[N], root; bool vis[N];
vector <pair <i64, int>> vec[N];
i64 dis[N];
void getroot(int u, int ff, int n) {
int mx = 0;
siz[u] = 1;
for (auto [v, w] : e[u]) {
if (vis[v] || v == ff) continue;
getroot(v, u, n);
siz[u] += siz[v], mx = max(mx, siz[v]);
}
mx = max(mx, n - siz[u]);
if (mx * 2 <= n) root = u;
}
void dfs(int u, int ff, vector <pair <i64, int>> &vec) {
vec.emplace_back(dis[u], u);
for (auto [v, w] : e[u]) {
if (vis[v] || v == ff) continue;
dis[v] = dis[u] + w;
dfs(v, u, vec);
}
}
void conq(int u, int n) {
// cout << "enter : " << u << ", now size is " << n << "\n";
if (n == 1) return;
root = 0, getroot(u, 0, n);
vis[u = root] = true, dis[u] = 0;
// cout << "the root is " << root << "\n";
auto &v = vec[u];
dfs(u, 0, v);
sort(v.begin(), v.end());
for (int i = 0; i < n; i++) {
t[V + i + 1].emplace_back(v[i].second);
if (i) t[V + i + 1].emplace_back(V + i);
// cout << "link " << V + i + 1 << " -> " << v[i].second << "\n";
// cout << "link " << V + i + 1 << " -> " << V + 1 << "\n";
}
for (int i = 0, it; i < n; i++) {
it = v[i].second;
if (eff[it] >= dis[it]) {
int j = lower_bound(v.begin(), v.end(), make_pair(eff[it] - dis[it] + 1, 0)) - v.begin() - 1;
t[it].emplace_back(V + 1 + j);
// cout << "link " << it << " -> " << V + j + 1 << "\n";
}
}
V += n;
for (auto [v, w] : e[u]) {
if (vis[v]) continue;
conq(v, siz[v] < siz[u] ? siz[v] : n - siz[u]);
}
}
int dfn[M], low[M], tim, stk[M], tp, ins[M], cnb, col[M], cnt[M], mark[M];
void tarjan(int u) {
dfn[u] = low[u] = ++tim;
stk[++tp] = u, ins[u] = 1;
for (auto v : t[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (ins[v]) {
low[u] = min(low[u], dfn[v]);
}
}
if (low[u] == dfn[u]) { ++cnb;
int x = -1;
while (x != u) {
x = stk[tp--];
col[x] = cnb;
ins[x] = 0;
}
}
}
u32 rt[M], tot, _tot; int L;
struct dat {
u32 ls, rs, cnt : 31, full : 1;
} tr[S];
#define m ((l + r) >> 1)
void up(u32 x) {
auto ls = tr[tr[x].ls], rs = tr[tr[x].rs];
tr[x].cnt = ls.cnt + rs.cnt;
tr[x].full = ls.full & rs.full;
}
void add(u32 &x, int l, int r, int p, int k) {
if (!x) x = ++tot;
if (l == r) return tr[x].cnt += k, tr[x].full = 1, void();
if (p <= m) add(tr[x].ls, l, m, p, k);
else add(tr[x].rs, m + 1, r, p, k);
up(x);
}
void merge(u32 &x, u32 y, int l, int r) {
if (!x || !y || x == y) return x |= y, void();
if (tr[x].full) return;
if (tr[y].full) return x = y, void();
if (x <= _tot) tr[++tot] = tr[x], x = tot;
merge(tr[x].ls, tr[y].ls, l, m);
merge(tr[x].rs, tr[y].rs, m + 1, r);
up(x);
}
#undef m
signed main() {
ios :: sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) cin >> eff[i];
for (int i = 1; i < n; i++) {
i64 x, y, z; cin >> x >> y >> z;
e[x].emplace_back(y, z);
e[y].emplace_back(x, z);
}
V = n, conq(1, n);
for (int i = 1; i <= V; i++) if (!dfn[i]) tarjan(i);
for (int u = 1; u <= V; u++) {
for (auto v : t[u]) if (col[u] != col[v]) G[col[u]].emplace_back(col[v]);
}
for (int i = 1; i <= n; i++) ++cnt[col[i]];
for (int i = 1; i <= cnb; i++) if (cnt[i]) ins[i] = ++L;
for (int i = 1; i <= cnb; i++) if (cnt[i]) {
add(rt[i], 1, L, ins[i], cnt[i]);
}
fill(mark + 1, mark + cnb + 1, 0);
for (int u = 1; u <= cnb; u++) { _tot = tot;
for (auto v : G[u]) {
if (mark[v] == u) continue;
mark[v] = u, merge(rt[u], rt[v], 1, L);
}
mark[u] = 0;
}
for (int i = 1; i <= n; i++) cout << tr[rt[col[i]]].cnt << " \n"[i == n];
return 0;
}
[PA 2022] Płótno
\(2n\) 个方格,上下两排各 \(n\) 个,首尾相接连成环状。每个方格上有一个 \(1 \sim 2n\) 的数字,所有数字互不相同。对 \(v \in [1,k]\),求有多少个区间 \([l,r]\) 满足数字在 \([l,r]\) 内的方格组成的连通块数为 \(v\)。
\(n \leq 10^5\),\(k \leq 10\),时限 \(\text{4.0s}\)。
先回顾一下如果是树的话我们是怎么做的:点边容斥,然后直接扫描线,从大到小枚举左端点 \(i\),维护右端点 \(j\) 的答案,加点 \(a_i\) 是对 \([a_i,n]\) 后缀加 \(1\),加边 \((u_i,v_i)\) 是在枚举到 \(\min(u_i,v_i)\) 的时候对 \([\max(u_i,v_i),n]\) 后缀减 \(1\),容易用线段树维护。
但现在这个东西可能是有环的,该怎么办呢。别忘了有平面图的欧拉公式,我们可以把它拍扁变成圆环,然后和上面一样做就行了,时间复杂度 \(\mathcal{O}(nk \log n)\)。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef vector <pair <int, int>> dat;
constexpr int N = 5e5 + 5;
int n, k, a[2][N]; LL ans[15];
dat v[N];
dat operator + (const dat &x, const dat &y) {
int i = 0, j = 0;
dat z;
while (i < (int)x.size() && j < (int)y.size() && (int)z.size() <= k) {
if (x[i].first < y[j].first) {
z.emplace_back(x[i]), ++i;
} else if (x[i].first > y[j].first) {
z.emplace_back(y[j]), ++j;
} else {
auto [x1, y1] = x[i]; ++i;
auto [x2, y2] = y[j]; ++j;
z.emplace_back(x1, y1 + y2);
}
}
while (i < (int)x.size() && (int)z.size() <= k) {
z.emplace_back(x[i]), ++i;
}
while (j < (int)y.size() && (int)z.size() <= k) {
z.emplace_back(y[j]), ++j;
}
return z;
}
struct SGT {
#define m ((l + r) >> 1)
dat tr[N << 2]; int tag[N << 2];
void add(int x, int k) {
tag[x] += k;
for (auto &i : tr[x]) i.first += k;
}
void down(int x) { if (tag[x]) add(x << 1, tag[x]), add(x << 1 | 1, tag[x]), tag[x] = 0; }
void build(int x, int l, int r) {
tr[x].assign(1, make_pair(N, r - l + 1));
if (l == r) return;
build(x << 1, l, m), build(x << 1 | 1, m + 1, r);
}
void mdf(int x, int l, int r, int p, int k) {
if (l == r) return tr[x].assign(1, make_pair(k, 1));
down(x);
if (p <= m) mdf(x << 1, l, m, p, k);
else mdf(x << 1 | 1, m + 1, r, p, k);
tr[x] = tr[x << 1] + tr[x << 1 | 1];
}
void add(int x, int l, int r, int ql, int qr, int k) {
if (ql <= l && qr >= r) return add(x, k);
down(x);
if (ql <= m) add(x << 1, l, m, ql, qr, k);
if (qr > m) add(x << 1 | 1, m + 1, r, ql, qr, k);
tr[x] = tr[x << 1] + tr[x << 1 | 1];
}
#undef m
} sgt;
signed main() {
ios :: sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> k;
for (int j = 0; j <= 1; j++) {
int mi = N, mx = 0;
for (int i = 1; i <= n; i++) {
cin >> a[j][i];
mi = min(mi, a[j][i]), mx = max(mx, a[j][i]);
}
v[mi].emplace_back(mx, 1);
}
int m = 2 * n;
v[1].emplace_back(m, -1);
a[0][n + 1] = a[0][1];
a[1][n + 1] = a[1][1];
for (int i = 1; i <= n; i++) {
v[min(a[0][i], a[1][i])].emplace_back(max(a[0][i], a[1][i]), -1);
v[min(a[0][i], a[0][i + 1])].emplace_back(max(a[0][i], a[0][i + 1]), -1);
v[min(a[1][i], a[1][i + 1])].emplace_back(max(a[1][i], a[1][i + 1]), -1);
v[min({ a[0][i], a[0][i + 1], a[1][i], a[1][i + 1]})].emplace_back(max({ a[0][i], a[0][i + 1], a[1][i], a[1][i + 1] }), 1);
}
sgt.build(1, 1, m);
for (int i = m; i >= 1; i--) {
sgt.mdf(1, 1, m, i, 0);
sgt.add(1, 1, m, i, m, 1);
for (auto [j, k] : v[i]) sgt.add(1, 1, m, j, m, k);
for (auto [x, y] : sgt.tr[1]) {
if (x <= k) ans[max(x, 1)] += y;
}
}
for (int i = 1; i <= k; i++) cout << ans[i] << " \n"[i == k];
return 0;
}
[PA 2022] Chodzenie po linie
给定一个长为 \(n\) 的排列 \(p\),按如下方式生成图 \(G\):若 \(i < j\) 且 \(p_i > p_j\),在 \(i\) 和 \(j\) 之间连接一条长为 \(1\) 的边。对每个点求它到所有点的最短路之和。如果无法到达则最短路为 \(0\)。
\(n \leq 2 \times 10^5\),时限 \(\text{6.0s}\)。
神题。放到平面上考虑这个问题,即将 \(i\) 号点视为 \((i,p_i)\),那么其连边范围为其左上和右下的所有点。
容易把整个序列划分为若干个区间,其中每个区间都是一个连通块。这些连通块之间互相独立,我们只考虑处理一个连通块的问题。
在这个图中,有一些点是比较特殊的:它们只有一个方向有连边。当然很容易发现它们正是前缀最大值和后缀最小值,我们找到这些点,可以发现它们像下图中这样形成两条边界:
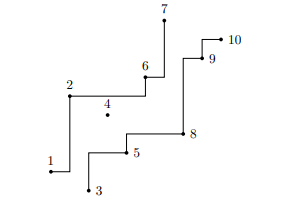
容易看出,每个点都至少和边界上的一个点有连边,或者它就在边界上。另一个容易发现的事实是,对于 \(i\) 左下方的点 \(j\),如果我们想从 \(i\) 到 \(j\),最优的走法一定是,先跳到某个边界上,然后跳到其能跳到的最左的位置或最下的位置(这取决于在哪个边界上,容易发现这样跳完之后会到另一个边界上),这样交替在两个边界上反复横跳,直到能够跳到 \(j\)。例如在上图中如果我们想从 \(10\) 到 \(1\),最优的方案是 \(10 \to 7 \to 8 \to 2 \to 3 \to 1\)。走回头路看起来就不优,感性理解一下它确实是对的。
于是我们就发现 \(i\) 左下和右上基本独立了,不失一般性我们考虑左下的部分怎么做。
我们把反复横跳的过程写得更形式化一些,设 \(c_i\) 表示 \(i\) 号点可达的下边界上最下的点,设 \(d_i\) 表示 \(i\) 号点可达的上边界上最左的点。关键的操作是,我们可以把每个点的贡献拆开,即对于每个 \(k\) 求出有多少个顶点 \(j(j < i)\) 和 \(i\) 的距离至少为 \(k\)。
容易发现,当 \(k=1\) 时答案是 \(i-1\)。而对 \(k > 1\) 的部分,我们对每个 \(i\) 依次枚举对 \((a_L,b_L)\),其中 \(a_1 = b_1 = i\),\(a_L = d_{b_{L-1}}, b_L = c_{a_{L-1}}\),那么 \(k=L+1\) 时的答案就是满足 \(j < a_L, p_j < p_{b_L}\) 的点 \(j\) 的数量。
由此我们可以得到一个 \(\mathcal{O}(n^2)\) 的做法:即做二维前缀和,对每个对 \(\mathcal{O}(1)\) 查询结果。但显然这是不够的。
有一个简单的观察是,\((a,b)\) 之间一定有连边,这点通过归纳不难证明。这也给了我们启示:也许可能的对数并不会太多?
事实上确实如此。关键的结论是:所有可能出现的 \((a,b)\) 的对的总数是 \(\mathcal{O}(n \sqrt n)\) 级别的!
我们来严谨地证明这个结论。首先,对于所有 \(i\),都有一个对 \((i,i)\),我们可以忽略这 \(n\) 个对。对于剩下的所有对,我们枚举 \(i\),设 \(i\) 右下方与 \(i\) 有连边的点分别为 \(b_1,b_2,\cdots,b_L\)(其中 \(b_1 = c_i,b_j < b_{j+1}\)),它们可以形成 \(L\) 个对 \((i,b_1),\cdots,(i,b_L)\)。在这 \(L\) 个对中,我们称前 \(\sqrt n\) 个对为一类对,其余的对为二类对。
由于每个点最多会有 \(\sqrt n\) 个一类对,因此一类对的总数是 \(\mathcal{O}(n \sqrt n)\) 的。而对于每个二类对 \((a,b)\) 和它跳到的下一个对 \((d_b,c_a)\),必然有 \(b - c_a \geq \sqrt n\),且 \(d_b < a\)。这意味着,每跳一次,\(a+b\) 的值至少减少了 \(\sqrt n\),而至多只能减少 \(\mathcal{O}(\sqrt n)\) 次——也就是说,对于每个点,二类对也只有 \(\mathcal{O}(\sqrt n)\) 个,二类对的总数也是 \(\mathcal{O}(n \sqrt n)\) 的!这就证明了结论。
利用单调性,通过适当的枚举顺序我们可以在 \(\mathcal{O}(n \sqrt n)\) 的时间内预处理出所有可能的对。同时我们可以发现所有对之间形成一颗内向树,每个位置对应的对是其到根的所有对。因此假设我们已经求出了每个对的答案,利用树的结构很容易能够求出每个位置的答案,具体实现可以参考代码理解。
最后的问题是如何快速查询满足 \(j < a,p_j < p_b\) 的点数。扫描线之后相当于是后缀加,单点查询,如果用线段树做时间复杂度是 \(\mathcal{O}(n \sqrt n \log n)\) 的,还是跑不过。注意到,后缀加只有 \(\mathcal{O}(n)\) 次,而查询的次数有 \(\mathcal{O}(n \sqrt n)\) 次,我们希望能够找到一个能够快速查询,但修改可以不需要太快的数据结构——\(\mathcal{O}(\sqrt n)\) 后缀加,\(\mathcal{O}(1)\) 查询的分块恰好可以完成这个任务。
总时间复杂度 \(\mathcal{O}(n \sqrt n)\)。不过如果提前告诉我正解复杂度是根号,我大概也猜不出来根号到底是怎么来的(笑),还是太菜了。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair <LL, LL> pi;
typedef vector <int> vi;
vector <pi> calc(vi p) {
int n = p.size() - 1;
vi q(n + 1);
for (int i = 1; i <= n; i++) q[p[i]] = i;
vi pmi(n + 2), qmi(n + 2);
pmi[n + 1] = qmi[n + 1] = n + 1;
for (int i = n; i >= 1; i--) {
pmi[i] = min(pmi[i + 1], p[i]);
qmi[i] = min(qmi[i + 1], q[i]);
}
vector <vector <pi>> vec(n + 2);
for (int i = n; i >= 1; i--) {
vec[i].insert(vec[i].begin(), {p[i], -1});
for (int j = 0; j < (int)vec[i].size(); j++) {
int b = vec[i][j].first;
int c = qmi[b];
int d = pmi[i];
if (!vec[c].empty() && vec[c].back().first == d) continue;
vec[c].emplace_back(d, -1);
}
}
vector <pi> res(n + 1);
int B = ceil(sqrt(n));
vi sum(n + 2);
vi pre(n + 2);
vi bak(n + 2);
for (int i = 1; i <= n; i++) {
bak[i] = (int)vec[i].size() - 1;
res[i].second = sum[(p[i] - 1) / B * B] + pre[p[i]];
for (int x = (int)vec[i].size() - 1; x >= 0; x--) {
auto &pa = vec[i][x];
int j = pa.first;
pa.second = sum[(j - 1) / B * B] + pre[j];
if (i == 1 && j == 1) continue;
int c = qmi[j];
int d = pmi[i];
while (vec[c][bak[c]].first != d) bak[c]--;
pa.second += vec[c][bak[c]].second;
}
int j = p[i];
while (1) {
pre[j]++;
if (j % B == 0 || j == n) break;
j++;
}
while (j < n) {
sum[j]++, j += B;
}
}
for (int i = 1; i <= n; i++) {
for (auto it : vec[i]) {
if (it.first == p[i]) {
res[i].first = it.second + res[i].second;
break;
}
}
}
return res;
}
void solve(vi p) {
int n = (int)p.size() - 1;
auto L = calc(p);
for (int i = 1; i <= n; i++) p[i] = n - p[i] + 1;
reverse(p.begin() + 1, p.end());
auto R = calc(p);
reverse(R.begin() + 1, R.begin() + n + 1);
for (int i = 1; i <= n; i++) {
cout << L[i].first + R[i].first + (n - 1 - L[i].second - R[i].second) << " ";
}
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(nullptr);
int n; cin >> n;
vi p(n + 2);
vi ed{ 0 };
int mx = 0;
for (int i = 1; i <= n; i++) {
cin >> p[i];
mx = max(mx, p[i]);
if (mx == i) ed.emplace_back(i);
}
for (int j = 1; j < (int)ed.size(); j++) {
int l = ed[j - 1] + 1;
int r = ed[j];
vi q{ 0 };
for (int i = l; i <= r; i++) {
q.emplace_back(p[i] - l + 1);
}
solve(q);
}
cout << "\n";
return 0;
}
[PA 2022] Nawiasowe podziały
给定一个长为 \(n\) 的不一定合法的括号串,划分成 \(k\) 段使得每段内合法括号序列子串数之和最小。
\(k \leq n \leq 10^5\),时限 \(\text{6.0s}\)。
比较无脑的 \(\mathcal{O}(n \log^3 n)\) 做法。
看到序列划分问题,老套路先检查一下代价是否满足四边形不等式。然后我们发现它确实满足,于是根据 这里的结论,答案关于 \(k\) 是凸的。
WQS 二分之后,由于本题代价比较难算,需要用决策单调性分治,用指针维护代价。一般的决策单调性题是分层转移,但由于我们并不需要知道每个 \(k\) 的答案,只要满足需要转移的两个部分之间有转移,而内部没有转移就可以利用决策单调性分治,于是我们直接 CDQ 分治就行了。总时间复杂度 \(\mathcal{O}(n \log^3 n)\)。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair <LL, int> pi;
constexpr int N = 1e5 + 5;
constexpr LL inf = 1e18;
int n, k;
string s;
int stk[N], tp, pr[N];
int cl, cr, id[N], cnt[N]; LL cur;
LL qry(int l, int r) {
while (cl > l) {
cl--;
if (s[cl] == '(' && pr[cl] <= cr) cnt[id[cl]]++, cur += cnt[id[cl]];
}
while (cr < r) {
cr++;
if (s[cr] == ')' && pr[cr] >= cl) cnt[id[pr[cr]]]++, cur += cnt[id[pr[cr]]];
}
while (cl < l) {
if (s[cl] == '(' && pr[cl] <= cr) cur -= cnt[id[cl]], cnt[id[cl]]--;
cl++;
}
while (cr > r) {
if (s[cr] == ')' && pr[cr] >= cl) cur -= cnt[id[pr[cr]]], cnt[id[pr[cr]]]--;
cr--;
}
return cur;
}
pi f[N]; LL K;
void trans(int l, int r, int ql, int qr) {
if (r < l) return;
int m = (l + r) >> 1;
pi t = f[ql];
t.first += qry(ql + 1, m) + K, t.second++;
int pos = ql;
for (int i = ql + 1; i <= qr; i++) {
pi _t = f[i];
_t.first += qry(i + 1, m) + K, _t.second++;
if (_t < t) t = _t, pos = i;
}
f[m] = min(f[m], t);
trans(l, m - 1, ql, pos);
trans(m + 1, r, pos, qr);
}
void cdq(int l, int r) {
if (l == 0 && r == n) for (int i = 1; i <= n; i++) f[i] = {inf, inf};
if (l == r) return;
int m = (l + r) >> 1;
cdq(l, m), trans(m + 1, r, l, m), cdq(m + 1, r);
}
signed main() {
ios :: sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> k;
cin >> s;
s = ' ' + s;
for (int i = 1; i <= n; i++) {
if (s[i] == '(') stk[++tp] = i;
else if (tp) {
pr[stk[tp]] = i;
pr[i] = stk[tp];
tp--;
}
}
while (tp) pr[stk[tp]] = n + 1, tp--;
int t = 0;
for (int i = 1; i <= n; i++) {
if (s[i] == '(' && !id[i]) {
t++;
for (int j = i; pr[j] && s[j] == '('; j = pr[j] + 1) id[j] = t;
}
}
cl = 1, cr = 0;
LL l = 0, r = 1e10;
while (l < r) {
LL m = (l + r) >> 1;
K = m;
cdq(0, n);
if (f[n].second > k) l = m + 1;
else r = m;
}
K = l;
cdq(0, n);
cout << f[n].first - k * K << "\n";
return 0;
}