前言

以下内容大多摘抄自 OI-Wiki 以及 \(\text{Alex\_Wei}\)----自动机相关还有我董晓大爹。

确定有限状态自动机(DFA)

形式化定义

一个 确定有限状态自动机(DFA) 由以下五部分组成：

1.字符集(\(\Sigma\)) , 该自动机只能输入这些字符
2.状态集合(\(Q\)) , 如果把一个 \(DFA\) 看成一张有向图，那么 \(DFA\) 中的状态就相当于图上的顶点。
3.起始状态(\(start\)) , \(start\in Q\)，是一个特殊的状态。起始状态一般用 \(s\) 表示，为了避免混淆，本文中使用 \(start\)。
4.接受状态集合(\(F\)) , \(F \in Q\) , 是一组特殊的状态。
5.转移函数(\(\delta\)) , \(\delta\) 是一个接受两个参数返回一个值的函数，其中第一个参数和返回值都是一个状态，第二个参数是字符集中的一个字符。如果把一个 \(DFA\) 看成一张有向图，那么 \(DFA\) 中的转移函数就相当于顶点间的边，而每条边上都有一个字符。

\(DFA\) 的作用就是识别字符串，一个自动机 \(A\)，若它能识别（接受）字符串 \(S\)，那么 \(A(S)=\mathrm{True}\)，否则 \(A(S)=\mathrm{False}\)。

当一个 \(DFA\) 读入一个字符串时，从初始状态起按照转移函数一个一个字符地转移。如果读入完一个字符串的所有字符后位于一个接受状态，那么我们称这个 \(DFA\) 接受这个字符串，反之我们称这个 \(DFA\) 不接受 这个字符串。

如果一个状态 \(v\) 没有字符 \(c\) 的转移，那么我们令 \(\delta(v,c)=\mathrm{null}\)，而 \(\mathrm{null}\) 只能转移到 \(\mathrm{null}\)，且 \(\mathrm{null}\) 不属于接受状态集合。无法转移到任何一个接受状态的状态都可以视作 \(\mathrm{null}\)，或者说，\(\mathrm{null}\) 代指所有无法转移到任何一个接受状态的状态。

我们扩展定义转移函数 \(\delta\)，令其第二个参数可以接收一个字符串：\(\delta(v,s)=\delta(\delta(v,s[1]),s[2..|s|])\)，扩展后的转移函数就可以表示从一个状态起接收一个字符串后转移到的状态。那么，\(A(s)=[\delta(start,s)\in F]\)。

如，一个接受且仅接受字符串 "a", "ab", "aac" 的 \(DFA\)：

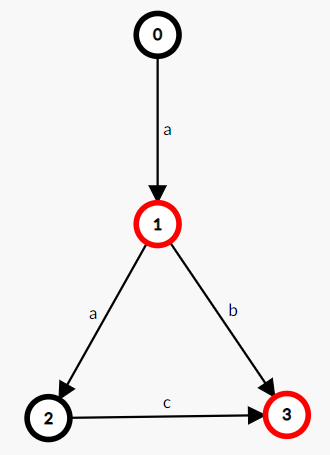
常见自动机

字典树

字典树接受且仅接受指定的字符串集合中的元素，说白了就是你输入啥它就怎么建树。

转移函数就是 \(Trie\) 上的边，接收状态是将每个字符串插入到 \(Trie\) 时到达的那个状态。也就是常用的 \(en[i]\) 数组。

ACAM AC自动机

AC 自动机也是一类常用的DFA，有完整的 DFA 五要素，分别是起点 \(start\)(Trie 树根节点)，状态集合 \(Q\)(Trie 树上所有节点)，接受状态集合 \(F\)(所有以某个单词作为后缀的节点,也就是\(en\)所在的位置)，字符集 \(\Sigma\)（题目给定）和转移函数 \(\delta\)(类似 KMP)。

解决问题

AC 自动机用于解决 多模式串 匹配问题：给定多个模式串 \(s_i\) 和一个文本串 \(t\) ，求 \(s_i\) 在 \(t\) 中出现的次数。由此可以看出，AC自动机和KMP的区别就在于模式串的多少。

算法详解

如果直接用 KMP 进行暴力，复杂度是 \(|t| \times N + \Sigma |s_i|\) ，其中 \(N\) 是单词个数。如果文本串 \(|t|\) 过长，那复杂度肯定就寄了。

步骤1：建 trie 树

这部分的操作就是用模式串建立字典树来进行操作。

步骤2：Fail指针的建立

类似于 KMP 中的 \(next\) 数组，感谢董晓大爹。

用白话说，Fail 指针的定义是：如果一个点 \(i\) 的 Fail 指针指向 \(j\) ，那么 \(root\) 到 \(j\) 的这个字符串就是 \(root\) 到 \(i\) 的字符串在这个 Trie 树里的最长后缀。

废话不多说，放图：

图中 \(Fail[6] = 2 , Fail[7] = 3\),这就是 Fail 指针的定义，下面我们考虑如何建立 Fail 指针。

首先我们要知道两个点

一、\(Trie[u][i]\) 可能有两种含义：

1.存节点 \(u\) 的树边的终点。如图中 \(ch[6][e] = 7\) ;

2.存节点 \(u\) 的转移边的终点，如 \(ch[7][r] = 4\) ，因为这种边在图中太多了，就没有表示出来。

二、这棵 Trie 树包含三种边，回跳边 、转移边 和树边。

(1)树边:树边就是我们在第一步建立 Trie 树形成的边；

(2)回跳边:回跳边指向父节点的回跳边所指节点的儿子，四个点(\(u,v,fail[u],trie[fail[u]][v]\))构成一个四边形。实际上我们就是通过这个思想来构建 Fail 指针的。回跳边的方向就是 Fail 指针的方向，并且这种边并不实际存在。所以我们可以发现 \(Fail[i]\) 就是存的节点 \(i\) 的回跳边的终点；

(3)转移边:转移边指向当前节点的回跳边所指节点的儿子，三个点(\(u,fail[u],trie[fail[u][v]\))构成一个三角形。我们通过建立这种边来完成最后文本串的遍历。

那么什么时候建回跳边，什么时候建转移边呢?我们看图说话。

如图：

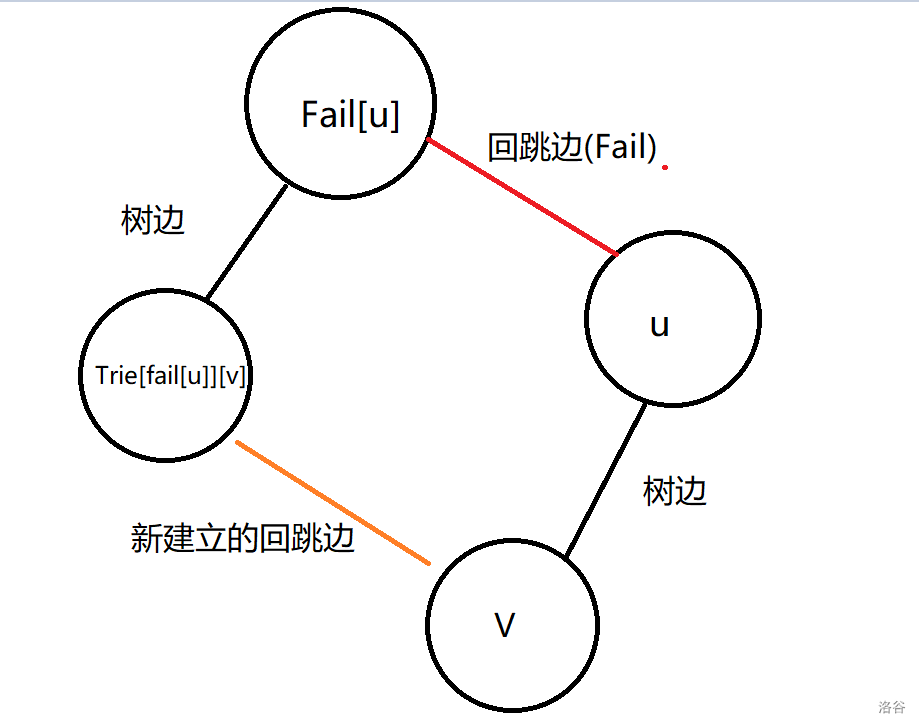
当 \(u\) 真实存在一个儿子节点 \(v\) 时，我们就建立回跳边来更新我们的 \(Fail\) 指针。那如果说不存在 \(Trie[fail[u]][v]\) 这个点怎么办？先不急，我们先看怎么建转移边。

如图：

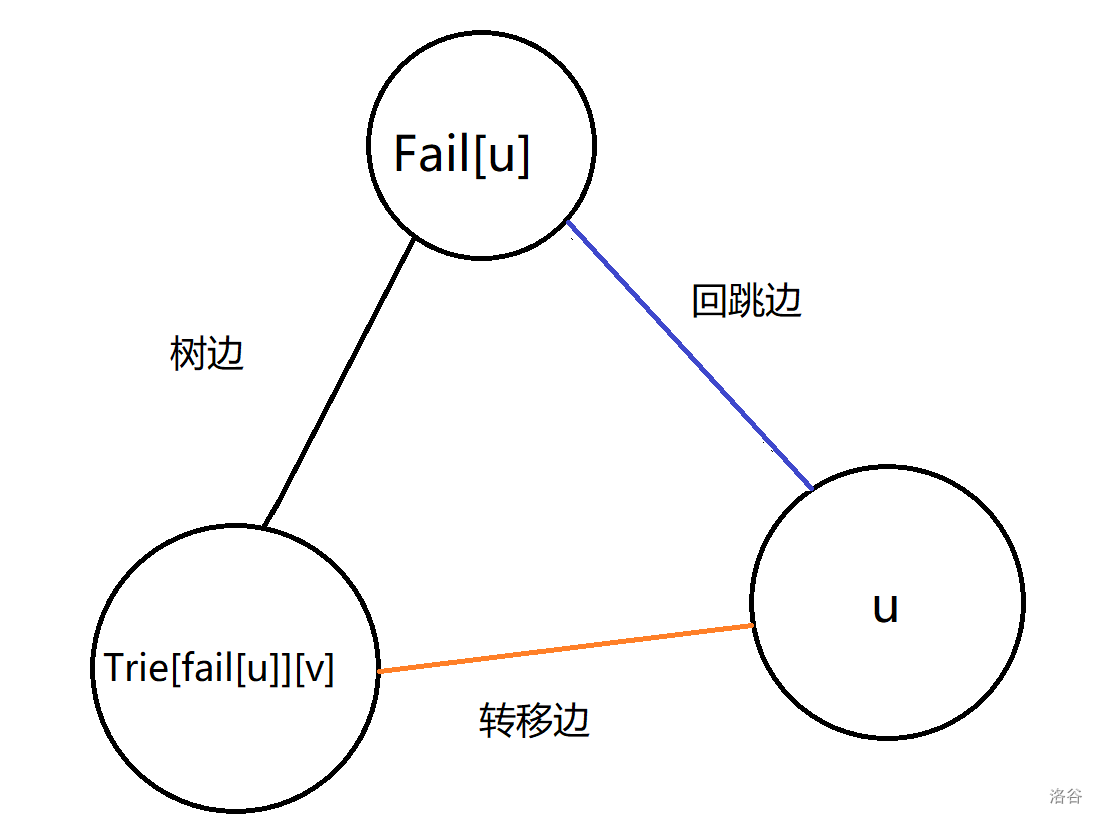
当 \(u\) 不存在一个真实的儿子节点 \(v\) 时，因为 \(u\) 和 \(Fail[u]\) 所处的位置都是同一个字母，所以其实它们是等价的，\(Fail[u]\) 存在一个儿子 \(v\) ，那么 \(u\) 也能存在一个儿子 \(v\) ，我们建立一个转移边。通过这样的连边，我们就能完成从一个分支上跳到另一个分支上的功能了。那如果 \(Trie[fail[u]][v]\) 也不存在呢？那么 \(u\) 就会通过这条转移边一直往上转移，知道找到一个真正的 \(v\) 点，或是一直转移到 \(root\) 也不存在，那么就会连向 \(root\)

怎么理解呢，还是看图：

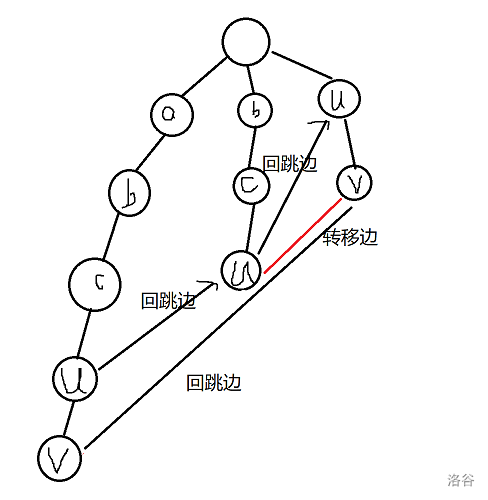
我们想给最下面的 \(v\) 建立 Fail 指针，就需要它的父亲 \(u\) 的回跳边所指节点的儿子 \(v\) ，可是 \(Fail[u]\) 并没有一个真实的子节点 \(v\) ，但是 \(Fail[Fail[u]]\) 有啊，并且在这之前我们已经建立了 \(Fail[u]\) 连向 \(Trie[Fail[Fail[u]]][v]\) 的一条转移边
，我们就能得到

\(Trie[Fail[u][v] = Trie[Fail[Fail[u]]][v]\) 了，那么又因为回跳边的定义

\(Fail[v] = Trie[Fail[u]][v]\) ，

我们最终便能得出 \(Fail[v] = Trie[Fail[Fail[u]]][v]\)，这就是我说的不断向上转移的过程。由此，刚才我提出的不存在 \(Trie[u][v]\) 这个点怎么建立回跳边的问题，就这么解决了。

如果你还是不能理解，一个个对应一下，仔细一点就好了。

通过上述的过程我们可以看出，回跳边和转移边的建立是有赖于深度较小的点的。因此，我们在建立 Trie 树的时候，是采取的 BFS 的方法来进行操作的。

至此，我们总结一下 \(Fail\) 指针的建立过程。

把深度为 \(1\) 的真实节点入队，因为它们的 Fail 指针肯定指向 root
节点 \(u\) 出队，枚举 \(u\) 的 \(26\) 个儿子

1.若儿子真实存在，建回跳边，把儿子入队

2.若非真实存在，节点 \(u\) 自建转移边。

Code:

il void Fail()
{
	queue <int> q;
	for(re int i=1;i<=26;i++) if(trie[0][i]) q.push(trie[0][i]);
	while(!q.empty())
	{
		int u = q.front();
		q.pop();
		for(re int i=1;i<=26;i++)
		{
			if(trie[u][i]) fail[trie[u][i]] = trie[fail[u]][i] , q.push(trie[u][i]);
			else trie[u][i] = trie[fail[u]][i];
		}
	}
}

步骤3：查询单词出现个数

扫描文本串，依次取出字符 \(s_i\)

\(i\) 指针走主串对应的节点，沿着树边或者是 转移边 走，保证不回退。
\(j\) 指针沿着回跳边搜索模式串，每次从当前节点走到根节点，把当前节点中的所有后缀模式串 一网打尽，保证不漏解。
扫描完主串，返回答案。

(董晓大爹的评论："算法一边走文本串，一边把当前穿的所有后缀串搜出来，实在是强。")

Code:

il void search(string s)
{
	int pos=0,len=s.size();
	for(int i=0;i<len;i++)
	{
		int ch=s[i]-'a'+1;
		pos=trie[pos][ch];
		for(int j=pos;j;j=fail[j]) ++cnt[en[j]];
	}
}