前言
都说数学来源于生活,又服务于生活,下面的案例就可以帮助我们理解这句话,也能摸索出高考以及模拟类考试中经常出现这样的有生活背景的数学题目,如果顺利去掉其生活背景,剩下的就是纯粹的数学模型了。
典例剖析
〖详解〗: 因为 \(t_1+t_2=2\), \(t_2+t_3=5\), \(t_3-t_1=T\), 所以 \(T=3\)。
又 \(T=\cfrac{2\pi}{\omega}\), 所以 \(\omega=\cfrac{2\pi}{3}\), 则 \(y=\sin(\cfrac{2 \pi}{3} t+\varphi)\),
由 \(0 \leq t \leq 60\), 则 \(\varphi \leq \cfrac{2 \pi}{3} t+\varphi \leq 40 \pi+\varphi\),
所以 1 分钟内阻尼器由其它位置摆动经过平衡位置的最多次数,等价于1分钟内 \(y=\sin(\cfrac{2 \pi}{3} t+\varphi)=0\) 的最多次数,等价于区间 \([\varphi, 40 \pi+\varphi]\) 里包含 \(k \pi(k \in Z)\) 的最多次数,
又 \(|\varphi|<\pi\), 则区间 \([\varphi, 40 \pi+\varphi]\) 里包含了 \(0\), \(\pi\), \(2\pi\), \(3\pi\), \(\ldots\), \(39\pi\) 或 \(\pi\), \(2\pi\), \(3\pi\), \(\ldots\), \(40\pi\),
所以区间 \([ \varphi, 40 \pi+\varphi ]\) 里包含 \(k \pi(k \in Z)\) 的最多次数为 40 。故选 \(C\) .
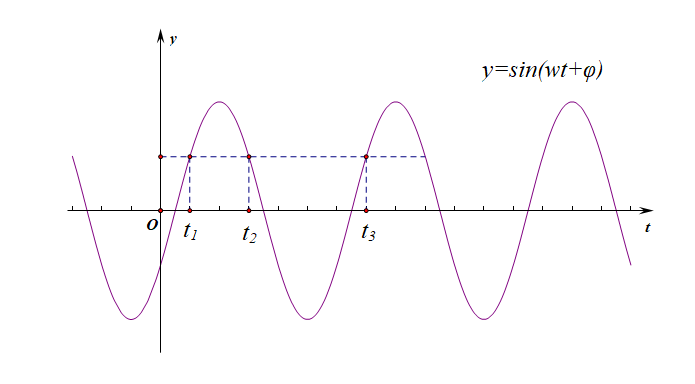
〖简解〗: 为便于理解题目意思,如下图所示,
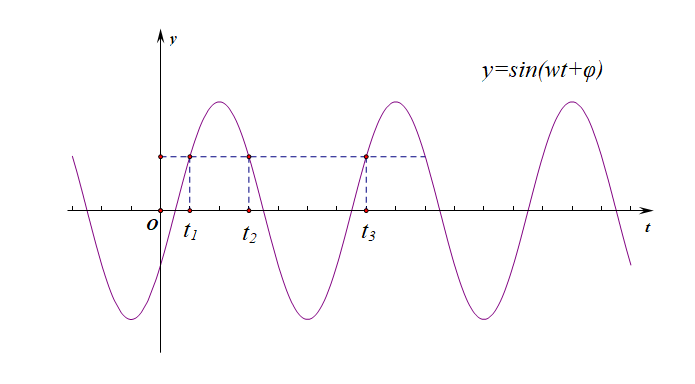
不妨设连续三次到达的同一位置都是平衡位置到最高点之间的某一个点,则连续三次到达这个点的时间点分别为 \(t_1\), \(t_2\), \(t_3\),则由 \(t_1+t_2=2\),\(t_2+t_3=5\),两式相减,得到 \(t_3-t_1=3\),而结合图像可知,\(t_3-t_1=T\),故\(T\)\(=\)\(3s\),那么频率 \(f\)\(=\)\(\cfrac{1}{T}\)\(=\)\(\cfrac{1}{3}\),即每秒摆动 \(\cfrac{1}{3}\) 个周期,又每个周期经过平衡位置的次数为 \(2\) 次,故 \(1\) 分钟内阻尼器由其它位置摆动经过平衡位置的次数最多为 \(60\)\(\times\)\(\cfrac{1}{3}\)\(\times2\)\(=\)\(40\),故选 \(C\) .
〖试题缺憾〗:由题目中 连续三次到达同一位置 这句话可知,当选择的位置为最高点或最低点时,
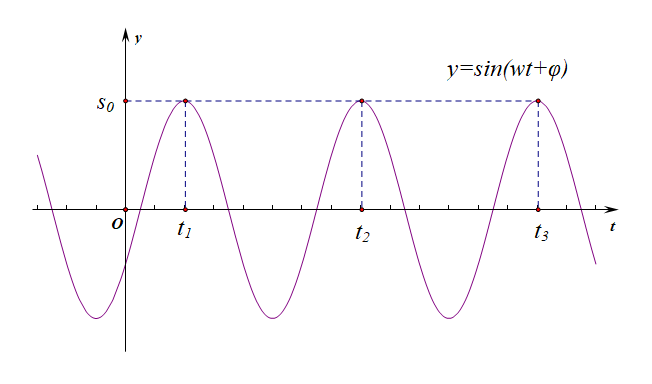
这时 \(t_1\)\(+\)\(t_2\)\(=\)\(2\),\(t_2\)\(+\)\(t_3\)\(=\)\(5\),但是 \(t_3\)\(-\)\(t_1\)\(=\)\(3\)\(=\)\(2T\),那么 \(T\)\(=\)\(\cfrac{3}{2}\),则仿照简解的思考过程可得, \(1\) 分钟内阻尼器由其它位置摆动经过平衡位置的次数最多为 \(60\)\(\times\)\(\cfrac{2}{3}\)\(\times2\)\(=\)\(80\),试题就出现了漏洞,后来在 菁优网 查询得到,有些题目对这句话替代为 “连续三次位移为 \(S_0\) ( \(-1<S_0<1\) )”,由于不是 \(-1\leqslant S_0\leqslant 1\),这样就排除了到达位置为最高点或者最低点的可能,试题就严谨多了。
试题引申
分析:如上求解,得到 \(\omega=\cfrac{2\pi}{3}\),
分析:由 \(t_1+t_2=2\)可知,\(\cfrac{t_1+t_2}{2}=1\),即 \(t=1\) 为 \(y=\sin(\cfrac{2\pi}{3}t+\varphi)\)的一条对称轴,
故有 \(\cfrac{2\pi}{3}\times 1+\varphi=k\pi+\cfrac{\pi}{2}\),解得 \(\varphi=k\pi-\cfrac{\pi}{6}\),\(k\in Z\),
令 \(k=0\),解得 \(\varphi=-\cfrac{\pi}{6}\in(-\pi,\pi)\),即解析式为 \(y=\sin(\cfrac{2\pi}{3}t-\cfrac{\pi}{6})\) .
由上述解析式可以求解,本题目解答略;
引申:求函数 \(y=\sin(\pi t-\cfrac{\pi}{2})\)的单调区间[此处有难点];
分析:求得单调递增区间为 \([2k,2k+1]\),单调递减区间为 \([2k+1,2k+2]\),则单调区间为 \([k,k+1]\)(不太好想,可以抽象问题具体化,赋值试试看);涉及到合二为一的考查;
解析: 因为 \(t_1+t_2=2\), \(t_2+t_3=5\), \(t_3-t_1=T\), 所以 \(T=3\), 又 \(T=\cfrac{2\pi}{\omega}\), 所以 \(\omega=\cfrac{2\pi}{3}\),
则 \(y=\sin(\cfrac{2\pi}{3} t+\varphi)\), 由 \(y>0.5\) 可得 \(\sin(\cfrac{2\pi}{3}t+\varphi)>0.5\),
所以 \(2k\pi+\cfrac{\pi}{6}<\cfrac{2\pi}{3} t+\varphi<\cfrac{5\pi}{6}+2k\pi\), \(k\in Z\),
\(3k+\cfrac{1}{4}-\cfrac{3}{2\pi} \varphi<t<\cfrac{5}{4}-\cfrac{3}{2\pi} \varphi+3k\), \(k\in Z\),
因为 \(\left(3 k+\cfrac{5}{4}-\cfrac{3}{2 \pi} \varphi\right)-\left(3k+\cfrac{1}{4}-\cfrac{3}{2\pi} \varphi\right)=1\),
所以在一个周期内阻尼器离开平衡位置的位移大于 \(0.5m\) 的总时间为 \(1s\).
实例演示
以下嵌入的别人的课件,可以帮助你理解题目中的 “某阻尼器的运动过程可近似为单摆运动”,如果出现“受限查看”,可以刷新一下再演示。