观察一下题目,如果没有车,求一个单源最短路就行了(但不要使用一种广为人知的最短路算法)
现在考虑有车的情况,显然最优策略是坐车到离\(1\)号节点最近的车能去的点下车。于是我们还是可以预处理每个点到\(1\)号节点的最短路,每次从节点\(v\)开始广搜它能去的所有海拔大于\(p\)的节点,时间复杂度\(O(Qn)\),瓶颈在于广搜
在回顾一下,我们所求的是离\(1\)号节点最近的海拔大于一个值的点,完全不需要用广搜维护。如果是离线可以带权并查集,但是这题在线。有没有一种树形结构满足权值单调呢,并且子树内的点都可以不依靠子树外的节点联通——\(Kruskal\)重构树完美满足。
我们按照边的海拔从大到小排序,建树,用下面的树演示一下如何计算答案。
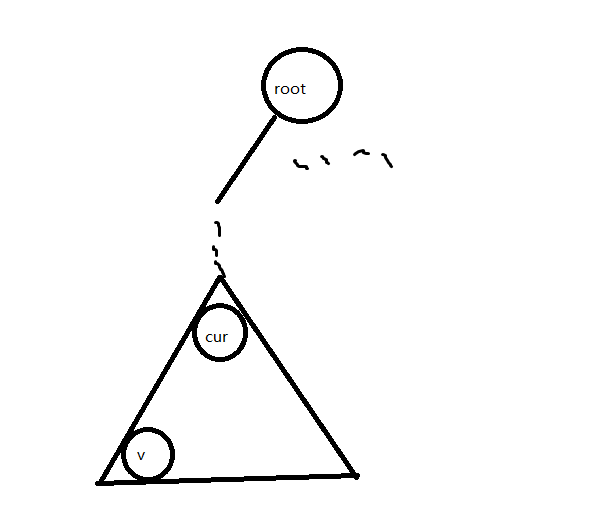
\(cur\)是出发节点\(v\)的一个祖先,如果\(cur\)的海拔大于\(p\),那么\(cur\)子树内的点都是联通的(车可以到达),因为权值单调,\(cur\)子树内的点肯定海拔也大于\(p\)。
贪心地,\(cur\)子树内的点肯定越多越好,也就是说\(cur\)是\(v\)的祖先里离根节点最近的海拔大于\(p\)的节点。怎么找\(cur\)?用倍增跳就行了(别忘了权值单调)。找到了\(cur\)以后,\(cur\)子树内最小\(dis\)值(预处理的最短路)就是答案
现在只剩最后一个问题,怎么找一个子树内最小的\(dis\)值?
这很简单,反正建完树以后树又不会变,预处理\(dfs\)一下就行了。
最短路\(O(mlongm)\),\(kruskal O(mlogm)\),倍增\(O(NlongN)\)。
ps:因为\(Kruskal\)重构树的节点数是\(N=2\times n+1\),所以不要忘了双倍空间
\(CODE\):
#include<bits/stdc++.h>
#define int long long
using namespace std;
int t;
int nows;
int fa[800001];
int n,m;
int q,k,s;
int lastans;
struct stu{
int from,to,val,h;
bool operator<(const stu &kl)const{
return h>kl.h;
}
}edge[800001];
struct node{
int x,dis;
bool operator<(const node &kl)const{
return dis>kl.dis;
}
};
int tree[800001],dp[800001][30],dep[800001],dis[800001],ans[800001];
bool vis[800001];
vector<node> nbr[800001];
vector<int> line[800001];
int find(int xx){
if(fa[xx]==xx) return xx;
else return fa[xx]=find(fa[xx]);
}
void dijkstra(int s){
memset(vis,0,sizeof(vis));
memset(dis,0x3f,sizeof(dis));
dis[s]=0;
node cur={s,dis[s]};
priority_queue<node> pq;
pq.push(cur);
while(!pq.empty()){
cur=pq.top();
pq.pop();
int x=cur.x;
if(vis[x]==true) continue;
vis[x]=true;
for(int i=0;i<nbr[x].size();i++){
int y=nbr[x][i].x;
int d=nbr[x][i].dis;
if(dis[y]>dis[x]+d){
dis[y]=dis[x]+d;
node nxt={y,dis[y]};
pq.push(nxt);
}
}
}
return ;
}
void kruskal(){
sort(edge+1,edge+1+m);
nows=n;
for(int i=1;i<=m;i++){
int x=find(edge[i].from);
int y=find(edge[i].to);
if(x!=y){
nows++;
tree[nows]=edge[i].h;
fa[x]=fa[y]=fa[nows]=nows;
line[nows].push_back(x);
line[nows].push_back(y);
}
}
}
void dfs(int now){
ans[now]=dis[now];
for(int i=0;i<line[now].size();i++){
dfs(line[now][i]);
ans[now]=min(ans[now],ans[line[now][i]]);
}
return;
}
void get_lca(int now,int fa){
dep[now]=dep[fa]+1;
dp[now][0]=fa;
for(int i=1;(1<<i)<=dep[now];i++){
dp[now][i]=dp[dp[now][i-1]][i-1];
}
for(int i=0;i<line[now].size();i++){
get_lca(line[now][i],now);
}
return;
}
int help(int now,int h){
for(int i=23;i>=0;i--){
if(dp[now][i] && tree[dp[now][i]]>h) now=dp[now][i];
}
return ans[now];
}
signed main(){
cin>>t;
while(t--){
lastans=0;
memset(tree,0xcf,sizeof(tree));
memset(ans,0x3f,sizeof(ans));
memset(dp,0,sizeof(dp));
for(int i=1;i<=n+m;i++){
nbr[i].clear();
line[i].clear();
}
cin>>n>>m;
for(int i=1;i<=n;i++) fa[i]=i;
for(int i=1;i<=m;i++){
cin>>edge[i].from>>edge[i].to>>edge[i].val>>edge[i].h;
node fi={edge[i].to,edge[i].val};
nbr[edge[i].from].push_back(fi);
fi={edge[i].from,edge[i].val};
nbr[edge[i].to].push_back(fi);
}
dijkstra(1);
kruskal();
dfs(nows);
get_lca(nows,0);
cin>>q>>k>>s;
while(q--){
int v0,p0;
cin>>v0>>p0;
int v=(v0+k*lastans-1)%n+1;
int p=(p0+lastans*k)%(s+1);
//cout<<v<<" "<<p<<endl;
lastans=help(v,p);
cout<<lastans<<endl;
}
}
return 0;
}