普通DP回顾
DP是解决多阶段决策最优化问题的一种思想方法,即利用各个阶段之间的关系,逐个求解,最终求得全局最优解。我们通常需要确认原问题与子问题、动态规划状态、边界状态、状态转移方程。
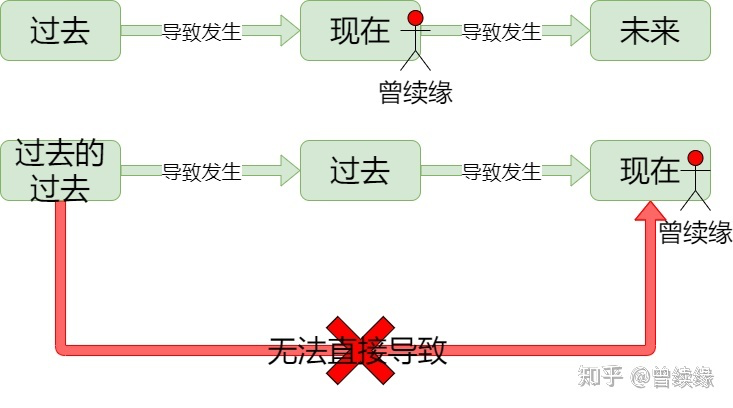
动态规划多阶段一个重要的特性就是无后效性,即“未来与过去无关”。无后效性就是对于某个给定的阶段状态,它以前各阶段的状态无法直接影响它未来的发展。换句话说,当前的状态是此前历史的一个完整总结,此前的历史只能通过当前的状态去影响过程未来的演变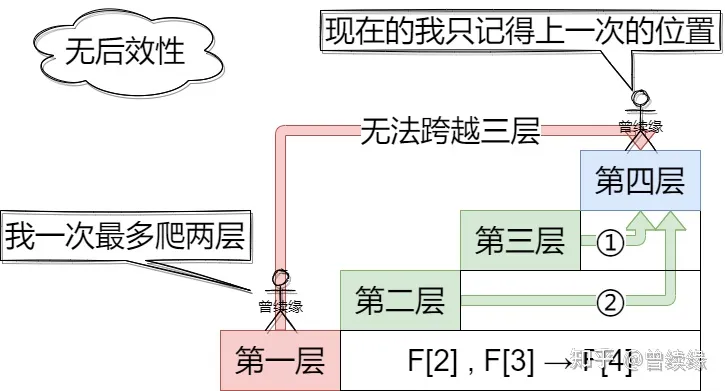
对于动态规划,如何定义状态是至关重要的,因为状态决定了阶段的划分,阶段的划分保证了无后效性。
状态压缩DP介绍
状态压缩DP其实是一种暴力的算法,因为它需要遍历每个状态,而每个状态是多个事件的集合,也就是说,状态压缩DP以集合为状态,一个集合就是一个状态。状态压缩DP的复杂度一般是指数的,因此用于小规模问题的求解

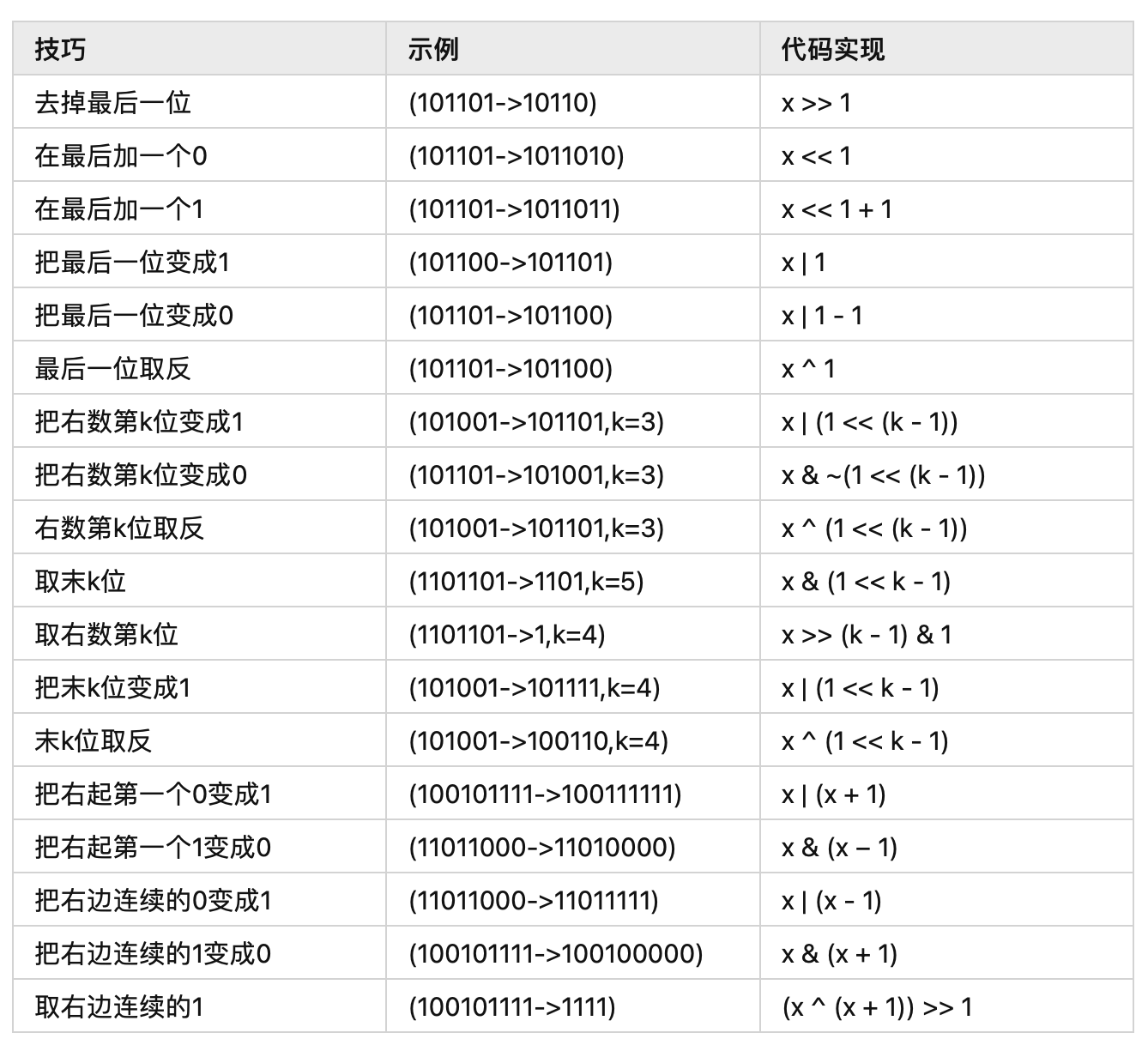
为了方便地同时表示一个状态的多个事件,状态一般用二进制数来表示。一个数就能表示一个状态,通常一个状态数据就是一个一串0和1组成的二进制数,每一位二进制数只有两种状态,比如说硬币的正反两面,10枚硬币的结果就可以用10位二进制数完全表示出来,每一个10位二进制数就表示了其中一种结果。使用二进制数表示状态不仅缩小了数据存储空间,还能利用二进制数的位运算很方便地进行状态转移。下面列举了一些常见的二进制位的变换操作。
例题1
题目描述
给你一个整数数组 cookies, 其中 cookies[i] 表示在第 i 个零食包中的饼干数量。另给你一个整数 k 表示等待分发零食包的孩子数量,所有 零食包都需要分发。在同一个零食包中的所有饼干都必须分发给同一个孩子,不能分开。
分发的不公平程度定义为单个孩子在分发过程中能够获得饼干的最大总数。
要求返回所有分发的最小不公平程度。
例1
输入:cookies = [8,15,10,20,8], k = 2
输出:31
解释:一种最优方案是 [8,15,8] 和 [10,20] 。
- 第 1 个孩子分到 [8,15,8] ,总计 8 + 15 + 8 = 31 块饼干。
- 第 2 个孩子分到 [10,20] ,总计 10 + 20 = 30 块饼干。
分发的不公平程度为 max(31,30) = 31 。
可以证明不存在不公平程度小于 31 的分发方案。
示例2
输入:cookies = [6,1,3,2,2,4,1,2], k = 3
输出:7
解释:一种最优方案是 [6,1]、[3,2,2] 和 [4,1,2] 。
- 第 1 个孩子分到 [6,1] ,总计 6 + 1 = 7 块饼干。
- 第 2 个孩子分到 [3,2,2] ,总计 3 + 2 + 2 = 7 块饼干。
- 第 3 个孩子分到 [4,1,2] ,总计 4 + 1 + 2 = 7 块饼干。
分发的不公平程度为 max(7,7,7) = 7 。
可以证明不存在不公平程度小于 7 的分发方案。
题解1

这里有两个问题。首先是sum的求法:sum是集合的元素和,我们先给出代码,如下所示:
int n = cookies.size();
vector<int> sum(1 << n);
for(int i=0;i<n;i++)
{
for(int j = 0, c = (1 << i); j < c ; j++)
{
sum[j|c] = sum[j] + cookies[i];
}
}
由于数组长度为n,因此不同的集合有 \(2^n\) 种,故我们设置sum的长度为 \(2^n\),以一个数字编号代表一种集合(而一种集合也就对应着一个状态)。
for(int j = 0, c = (1 << i); j < c ; j++)
上面这段代码表示c的二进制表示的第i位为1,然后j从0遍历到c-1,则sum[j|c]相当于填满了\(sum[2^i]-sum[2^{i+1}-1]\) ,共有 \(2^i\) 项,即计算 \(sum[2^i]-sum[2^{i+1}-1]\) 需要用到 \(sum[0]-sum[2^i-1]\). 作为示例,下面是当n=3时 sum代表元素的变化情况:
另一个问题是如何枚举 \(j\) 的子集 \(s\). 我们知道对于一个数 \(s\),\(s - 1\) 是将其二进制的最后一位置0. 我们不断让s=(s-1)&j 直至 \(s=0\),即可求出 \(j\) 的所有子集。为了从集合 \(j\) 中剔除掉子集 \(s\),可以采用异或的操作。最终代码如下:
class Solution {
public:
int distributeCookies(vector<int>& cookies, int k) {
int n = cookies.size();
vector<int>sum(1<<n);
for(int i=0;i<n;i++)
{
for(int j = 0, c = (1 << i); j < c ; j++)
{
sum[j|c] = sum[j] + cookies[i];
}
}
vector<vector<int> > f(k,vector<int>(1 << n, INT_MAX));
for(int i = 0; i < (1 << n); i++)
{
f[0][i] = sum[i];
}
for(int i = 1; i < k; i++){
for(int j = 1; j < (1 << n); j++){
for(int s = j; s ; s = (s - 1) & j)
{
f[i][j] = min(f[i][j], max(f[i-1][j^s], sum[s]));
}
}
}
return f[k - 1][(1 << n) - 1];
}
};
例二
[蓝桥杯 2019 省 A] 糖果
题目描述
糖果店的老板一共有 \(M\) 种口味的糖果出售。为了方便描述,我们将 \(M\) 种口味编号 \(1\) ∼ \(M\)。
小明希望能品尝到所有口味的糖果。遗憾的是老板并不单独出售糖果,而是 \(K\) 颗一包整包出售。
幸好糖果包装上注明了其中 \(K\) 颗糖果的口味,所以小明可以在买之前就知道每包内的糖果口味。
给定 \(N\) 包糖果,请你计算小明最少买几包,就可以品尝到所有口味的糖果。
输入格式
第一行包含三个整数 \(N\)、\(M\) 和 \(K\)。
接下来 \(N\) 行每行 \(K\) 这整数 \(T_1,T_2, \cdots ,T_K\),代表一包糖果的口味。
输出格式
一个整数表示答案。如果小明无法品尝所有口味,输出 \(-1\)。
样例 #1
样例输入 #1
6 5 3
1 1 2
1 2 3
1 1 3
2 3 5
5 4 2
5 1 2
样例输出 #1
2
提示
对于 \(30\%\) 的评测用例,\(1 \le N \le 20\)。
对于所有评测样例,\(1 \le N \le 100\),\(1 \le M \le 20\),\(1 \le K \le 20\),\(1 \le T_i \le M\)。
蓝桥杯 2019 年省赛 A 组 I 题。
题解
如果明白了第一个例题的话,这个例题也应该比较好理解。
设dp[i]为凑齐第i号集合所需的最少糖果包数。状态压缩的对象是把每一包糖果,把每包糖果看成一个集合,把这个集合用一个整数表示,该整数的最大值为1<<m,这个整数的二进制形式的第i位为1表示这包糖果里有第i种糖果。
代码如下:
#include <iostream>
#include<algorithm>
#include<set>
using namespace std;
int n, m, k;
set<int> st;
int dp[1 << 21];
int a[101];
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m >> k;
for(int i = 0; i < (1 << m); i++)
dp[i] = 0x3ffffff;
for(int i = 0; i < n; i++)
{
int x = 0, y;
for(int j = 0; j < k; j++)
{
cin >> y;
st.insert(--y);
//压缩成二进制数
x |= (1 << y);
}
//x的二进制表示中第k位为1代表这个这包糖中含有第k+1种糖
a[i] = x;
dp[x] = 1;
}
//n包糖果中的种类数小于m
if(int(st.size()) < m)
{
cout << -1;
return 0;
}
for(int i = 0; i < n; i++)
{
for(int status = 0; status < (1 << m); status++)
{
//当前已有的糖果加上第status包糖果
int next = a[i] | status;
dp[next] = min(dp[next], 1 + dp[status]);
}
}
cout << dp[(1 << m) - 1];
return 0;
}