description
给定整数 \(n,m\leq 10^6\)
求以 \((0,0)\) 为左下角,\((n,m)\) 为右上角构成的区域内每个格子被包含在的简单正方形(顶点都在区域内且在格点上的正方形)的数量之和。
模大质数
solution
先考虑一个简单一些的问题。
一个 \(n\times n\) 的正方形,求所有四个顶点分别在这个正方形四条边上的正方形所完整包含的格子的数量,记作 \(f(n)\)。
也就是下图所有粉色正方形完全包含的格子的数量。
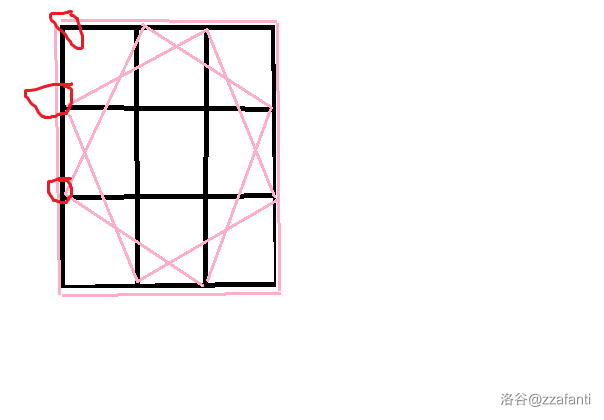
我们可以枚举 \(i\),从 \(0\) 到 \(n-1\),表示这个正方形在左边的顶点(图中画红圈的)距大正方形左上角距离。
当 \(i=1\) 时,显然有 \(n^2\) 个被完整包含的格子。
然后,我们只需要考虑每个斜着的正方形所完整包含的格子了。
如下图所示,一个斜着的正方形可以拆成中间一个正方形(灰色阴影部分)和四周四个全等的直角三角形。
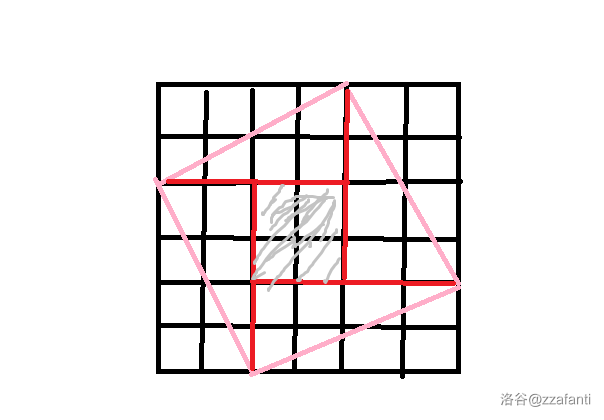
中间正方形的所包含的格子显然是 \((n-2i)^2\) 个(\(n-2i<0\) 也是这样的)。
问题变成一个直角边长度分别为 \(a,b\) 的直角三角形内部包含几个完整的方格,答案记作 \(g(a,b)\)。
不难看出,直角三角形每个内部和斜边(不含两端点)的格点都对应一个完整的格子。
所以把 \(g(a,b)\) 拆成两部分计算。斜边上的整点数量显然是 \(\gcd(a,b)-1\)。其内部的格点数量可由皮克定理(链接)得出为 \(\dfrac{ab-a-b-\gcd(a,b)+2}{2}\)。
加上斜边上的整点可知 \(g(a,b)=\dfrac{ab-a-b+\gcd(a,b)}{2}\)
于是 \(f(n)=n^2+\sum\limits_{i=1}^{n-1} (n-2i)^2+4g(i,n-i)\)
发现 \((n-2i)^2\) 和 \(g(i,n-i)\) 可以分开算。
主要说一下 \(\sum\limits_{i=1}^{n-1} g(i,n-i)\)
\(\begin{aligned} & \sum\limits_{i=1}^{n-1} g(i,n-i) \\ & =\sum\limits_{i=1}^{n-1} \dfrac{i(n-i)-i-(n-i)+\gcd(i,n-i)} {2} \\ & = \dfrac{1}{2}\sum\limits_{i=1}^{n-1}ni-i^2-n-\gcd(n-i,i) \\ & =\dfrac{1}{2}\sum\limits_{i=1}^{n-1}ni-i^2-n-\gcd(n,i) \end{aligned}\)
最后一步变形的依据是 \(\gcd(a,b)=\gcd(a,b-a)\)。
欧拉函数处理一下 \(\sum\limits_{i=1}^{n-1} \gcd(i,n)\) 就能算了。
我们现在求出了所有 \(f\) 的值,回到原题,我们只需枚举 \(x\),看哪些位置作为左下角可以放置 \(x\times x\) 的正方形,找到方案数,乘上 \(f(x)\) 即是答案,也就是 \(ans=\sum\limits_{x=1}^{\min(n,m)} (n-x+1)\times (m-x+1) \times f(x)\) 。
继续推。
\(\begin{aligned}ans= & \sum\limits_{x=1}^{\min(n,m)} (n-x+1)\times (m-x+1) \times f(x)\\ & =\sum\limits_{x=1}^{\min(n,m)} (x^2-(n+m+2)x+(nm+n+m+1))f(x)\end{aligned}\)
分别预处理 \(f(x),xf(x),x^2f(x)\) 的前缀和即可。
时间复杂度线性。
code
参考代码: Submission #222006907 - Codeforces
hint
推式子的时候加 1 减 1 之类的要很注意,容易出错。
去算某一部分的值时,放回原式不要把系数漏乘。
这道题的计数的思路是很有趣的。