点积又称内积,就是一种向量操作,把两个向量的元素对应相乘,然后把结果相加即可。
它可以计算相似性,还要从向量空间说起。向量就是一列数字,这一列有多少元素,就看成是多少维度的空间。
如向量a
array([[1], [2], [3], [4], [5], [6]])
那么我就可以把 a 看成是在一个6维空间的一个点。这么做的好处是点最简单啊,如果是一个二维的图像,你想有多少分类(三角形、长方形、菱形。。。),这些分类的每一种又有多少性质?总之,问题就复杂了,而一个点就简单了,独一无二,没有啥性质,唯一的性质就是它的坐标了,把问题简单化就是这么做的目的。
如果 a 点的坐标数据表示一个事物的属性值,那么如果事物 b 的属性值和 a 特别相似,就可以认为 a 和 b 特别相似。
这和点积有啥关系?这就是点积的另外一个公式: a·b=|a||b|cosθ ,其中|a| 代表空间中点 a 到原点的长度 |b|也类似。θ代表0a 和 0b的夹角,0代表原点。
如果两个点的长度相近,夹角接近0,那么就认为相似。
在夹角的区间[0,pi]中,cos的值在[-1,1]取值。
而长度那就没边了,可以取整个实数域。要把长度和夹角的权重都差不多才行,否则长度过大,就会不准。
解决办法就是把长度映射到区间[0,1]上,用指数函数,以e为底 e^{-x},当然这是原型,实际还要复杂一点。这样长度和夹角都有相等的权重,它们相乘的结果才会有相似度的度量功能。
这样,点积就可以度量相似性了,即点积值越大的,相似性越高。
上面虽然已经解决了,但有时长度过大,再加上指数函数的性质,导致点积值飞快的接近0,甚至出现下溢出的问题。
看指数的图像也可以看出来:
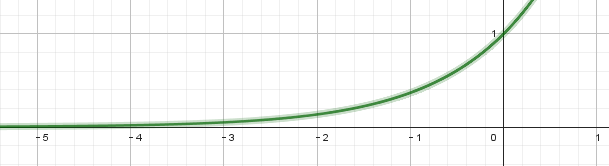
到 -5 的时候已经很接近 0 了,最好是把 x 的取值区间也控制一下,比如数值的取值范围大多在10万以内,维度是6,则除以 72 这样 x 数值就控制在1400以内了,这个 72 就是维度的平方乘以 2,故最后的归一公式这个样子:
np.exp(-0.5 * x^2/d^2)
参数也不宜过大,这样是指就都接近 1 了,总之一言以蔽之,中庸之道最好。